PARA VER LA VERSIÓN EN HTML RESPONSIVA DEL SCRIPT DE R CON GRÁFICAS INTERACTIVAS HAZ CLICK EN ESTA ORACIÓN
-
María Magdalena Castro Sam
-
Sergio Napoleón Leal
-
Jesús Omar Magaña Medina
-
Fernando Itzama Novales Campos
-
Adrián Ramírez Cortés
-
Efraín Soto Olmos
Éste código analiza algunos datos de la primera división de la liga española, obtenidos de https://www.football-data.co.uk/spainm.php. Más notas sobre los datos pueden encontrarse en https://www.football-data.co.uk/notes.txt.
🚀 Link para la aplicacion Shiny: https://omar-magaa.shinyapps.io/Postwork8/
🚀 Link para el video: https://www.youtube.com/watch?v=mOSzWZWkoHE
🚀 Link para el HTML interactivo: https://itzamango.github.io/postwork-equipo-10/
-
- 🔢 get.freq()
- 📋 Tablas de Frecuencias
- 🔢 get.prob.m.tbl()
- 📋 Probabilidad Marginal
- 🔢 get.prob.df() y get.round()
- 📋 Frecuencias y Probabilidad Marginal
- 🔢 get.prob.joint.tbl() y get.prob.joint.df
- 📋 Probabilidad Conjunta
-
- 📋 Importar datos
- 📋 Revisión de estructura de los Datos
- 📋 Selección de columnas
- 📋 Corrección y Unión de Datos
- 📋 Escritura de Archivo
-
- 📋 Local: Probabilidad Marginal
- 🔢 plot.bar()
- 📊 Local: P(x) Marginal
- 📋 Visitante: Probabilidad Marginal
- 📊 Visitante: P(y) Marginal
- 📋 Probabilidad Conjunta P(x∩y)
- 🔢 plot.heatmap()
- 📊 Heat Map P(x∩y) Conjunta
-
- 📋 Probabilidad Marginal
- 📋 Producto de Probabilidades Marginales
- 📋 Probabilidad Conjunta P(x∩y)
- 📋 Cociente de Probabilidades
- 📋 Bootstrap
- 🔢 bootstraps() rsample
- 📋 Medias Muestrales
- 📋 Intervalos de confianza
- 🔢 plot.histogram()
- 📊 Histograma medias bootstrap
- 📊 Histograma original
- 📋 Pruebas t
- 🏁 Conclusiones
-
- 📋 Escribir soccer.csv
- 📋 fbRanks: anotaciones y equipos
- 📋 Ranking de Equipos
- 📋 Predicción Última Fecha
- 📋 Matriz de Confusión
- 🏁 Conclusiones
-
- 📋 Columna “sumagoles”
- 📋 Promedio por mes
- 📋 Serie de Tiempo
- 📊 Serie de Tiempo
- 📋 Modelo Aditivo
- 📋 Modelo Multiplicativo
- 🏁 Conclusiones
-
- 📋 Alojar match.data.csv a match_games
- 📋 Número de Registros
- 📋 Consulta Sintaxis Mongodb
- 📋 Cerrar Conexión
-
- 📋 Creamos el logo para la aplicación Shiny
- 📋 Definimos la UI para la aplicacion
- 📋 Definimos las funciones del servidor
Importamos las bibliotecas con las que trabajaremos:
library(dplyr)Importamos datos de la primera división 2019-2020:
data <- read.csv("https://www.football-data.co.uk/mmz4281/1920/SP1.csv")Vemos la ayuda del comando table:
?tableget.freq <- function(data, team, name.freq){
team <- enquo(team)
data %>%
pull(!!team) %>%
table(., dnn = name.freq)
}Extraemos las columnas, obtenemos la frecuencia marginal para el equipo de casa y visitante en una función. con table generamos una tabla que nos indica la frecuencia de los goles:
freq.m.local <-
get.freq(data, FTHG, "Freq.Home")
(freq.m.local)## Freq.Home
## 0 1 2 3 4 5 6
## 88 132 99 38 14 8 1
freq.m.visit <-
get.freq(data, FTAG, "Freq.Away")
(freq.m.visit)## Freq.Away
## 0 1 2 3 4 5
## 136 134 81 18 9 2
get.prob.m.tbl <- function(data, team, name.prob){
team <- enquo(team)
data %>%
pull(!!team) %>%
table %>%
prop.table -> prob.tbl
names(attributes(prob.tbl)$dimnames) <- name.prob
return(prob.tbl)
}La probabilidad marginal es la probabilidad de que ocurra un evento simple, por lo tanto estará dada por el número de goles sobre el total de los partidos.
Calcularemos la probabilidad de que el equipo que juegue en casa anote ’x’ goles en una función:
La probabilidad marginal de que el equipo que juega local anote x goles (x = 0, 1, 2, …)
prob.m.local <-
get.prob.m.tbl(data, FTHG, "Prob.Home")
(prob.m.local %>% round(3))## Prob.Home
## 0 1 2 3 4 5 6
## 0.232 0.347 0.261 0.100 0.037 0.021 0.003
La probabilidad marginal de que el equipo que juega como visitante anote y goles (y = 0, 1, 2, …)
En el caso del equipo vistante el procedimiento es análogo.
prob.m.visit <-
get.prob.m.tbl(data, FTAG, "Prob.Away")
(prob.m.visit %>% round(3))## Prob.Away
## 0 1 2 3 4 5
## 0.358 0.353 0.213 0.047 0.024 0.005
get.prob.df<- function(data, team, name.gol, name.prob){
team <- enquo(team)
data %>%
pull(!!team) %>%
table(., dnn = (name.gol)) %>%
as.data.frame %>%
mutate(!!name.prob := Freq/sum(Freq))
}get.round <- function(data, digits){
data %>% mutate_if(is.numeric, round, digits=digits)
}Obtenemos un dataframe con las frecuencias y probabilidades con una función y redondeamos:
data.local <- get.prob.df(data, FTHG, "Gol.Home", "Prob.Marginal")
(data.local %>% get.round(3))## Gol.Home Freq Prob.Marginal
## 1 0 88 0.232
## 2 1 132 0.347
## 3 2 99 0.261
## 4 3 38 0.100
## 5 4 14 0.037
## 6 5 8 0.021
## 7 6 1 0.003
data.visit <- get.prob.df(data, FTAG, "Gol.Away", "Prob.Marginal" )
(data.visit %>% get.round(3))## Gol.Away Freq Prob.Marginal
## 1 0 136 0.358
## 2 1 134 0.353
## 3 2 81 0.213
## 4 3 18 0.047
## 5 4 9 0.024
## 6 5 2 0.005
get.prob.joint.tbl <- function(data, team.h, team.a, name.h, name.a){
data %>%
{table( team.h, team.a, dnn = c(name.h, name.a)) } %>%
prop.table
}
get.prob.joint.df <- function(data, team.h, team.a, name.h, name.a){
data %>%
{table( team.h, team.a, dnn = c(name.h, name.a)) } %>%
prop.table %>%
unclass %>%
as.data.frame
}La probabilidad conjunta toma en cuenta la probabilidad de dos eventos sobre el total de resultados posibles.
Calcularemos la probabilidad conjunta de que el equipo local anote ‘x’ goles y el visitante’y’ goles (x = 0, 1, 2, …, y = 0, 1, 2, …) con una función:
table.prob.joint <-
get.prob.joint.tbl(data, data$FTHG, data$FTAG, "x (Home)", "y (Away)")
(table.prob.joint %>% round(3))## y (Away)
## x (Home) 0 1 2 3 4 5
## 0 0.087 0.074 0.039 0.021 0.005 0.005
## 1 0.113 0.129 0.084 0.013 0.008 0.000
## 2 0.103 0.092 0.053 0.008 0.005 0.000
## 3 0.037 0.037 0.018 0.005 0.003 0.000
## 4 0.011 0.013 0.011 0.000 0.003 0.000
## 5 0.005 0.008 0.008 0.000 0.000 0.000
## 6 0.003 0.000 0.000 0.000 0.000 0.000
Importamos bibliotecas:
library(dplyr)
library(magrittr)Ahora agregamos aún más datos. Utilizaremos los datos de las temporadas 2017/2018, 2018/2019 y 2019/2020.
Importamos los datos a una lista:
temporadas <- c( SP1.1718 = "https://www.football-data.co.uk/mmz4281/1718/SP1.csv"
, SP1.1819 = "https://www.football-data.co.uk/mmz4281/1819/SP1.csv"
, SP1.1920 = "https://www.football-data.co.uk/mmz4281/1920/SP1.csv"
) %>% lapply(read.csv)Revisamos su estructura:
Solo se muestran las primeras 6 líneas de la consola
get.info <- function(data){
data %>% str
data %>% head
data %>% summary
data %>% View
}temporadas["SP1.1718"] %>% get.info## List of 1
## $ SP1.1718:'data.frame': 380 obs. of 64 variables:
## ..$ Div : chr [1:380] "SP1" "SP1" "SP1" "SP1" ...
## ..$ Date : chr [1:380] "18/08/17" "18/08/17" "19/08/17" "19/08/17" ...
## ..$ HomeTeam : chr [1:380] "Leganes" "Valencia" "Celta" "Girona" ...
## ..$ AwayTeam : chr [1:380] "Alaves" "Las Palmas" "Sociedad" "Ath Madrid" ...
...
temporadas["SP1.1819"] %>% get.info## List of 1
## $ SP1.1819:'data.frame': 380 obs. of 61 variables:
## ..$ Div : chr [1:380] "SP1" "SP1" "SP1" "SP1" ...
## ..$ Date : chr [1:380] "17/08/2018" "17/08/2018" "18/08/2018" "18/08/2018" ...
## ..$ HomeTeam : chr [1:380] "Betis" "Girona" "Barcelona" "Celta" ...
## ..$ AwayTeam : chr [1:380] "Levante" "Valladolid" "Alaves" "Espanol" ...
...
temporadas["SP1.1920"] %>% get.info## List of 1
## $ SP1.1920:'data.frame': 380 obs. of 105 variables:
## ..$ Div : chr [1:380] "SP1" "SP1" "SP1" "SP1" ...
## ..$ Date : chr [1:380] "16/08/2019" "17/08/2019" "17/08/2019" "17/08/2019" ...
## ..$ Time : chr [1:380] "20:00" "16:00" "18:00" "19:00" ...
## ..$ HomeTeam : chr [1:380] "Ath Bilbao" "Celta" "Valencia" "Mallorca" ...
...
Vemos que hay un diferente formato de fechas en la temporada 17/18.
Seleccionamos sólo las columnas de interés:
columns <- c( "Date"
, "HomeTeam"
, "AwayTeam"
, "FTHG"
, "FTAG"
, "FTR"
)
temporadas %<>% lapply(select, all_of(columns)) Revisamos que las columnas sean del mismo tipo, corregimos el error de
formato y tipo de dato de la columna Date y unimos en un solo data
frame:
data <- temporadas %>% unname %>% do.call(rbind, .)
# Corrección del formato de fecha usando una expresión regular
data %<>% mutate(Date = gsub("/(1[78])$", "/20\\1", Date))
# Correccioón del tipo de dato
data %<>% mutate(Date = as.Date(Date, "%d/%m/%Y"))
head(data$Date)## [1] "2017-08-18" "2017-08-18" "2017-08-19" "2017-08-19" "2017-08-19"
## [6] "2017-08-20"
#data frame final solo con los datos elegidos
(dim(data))## [1] 1140 6
Guardamos el data frame obtenido en formato csv en una carpeta llamada “equipo10”:
w.dir <- getwd()
sub.dir <- "equipo10"
path <- file.path(w.dir, sub.dir)
dir.create(path, showWarnings = F, recursive = T)
setwd(path)
#guardamos el df en un archivo csv
write.csv(data, file = 'Postwork_02.csv', row.names = FALSE)
setwd(w.dir)Importamos las bibliotecas:
library(ggplot2)
library(plotly)
library(dplyr)
library(ggplot2)
library(viridis)
library(viridisLite)Con el data frame obtenido realizaremos algunas gráficas.
data <- "https://raw.githubusercontent.com/napoleonleal/R-BEDU-Project/main/Postwork_2/Postwork_02.csv" %>%
read.csv %>%
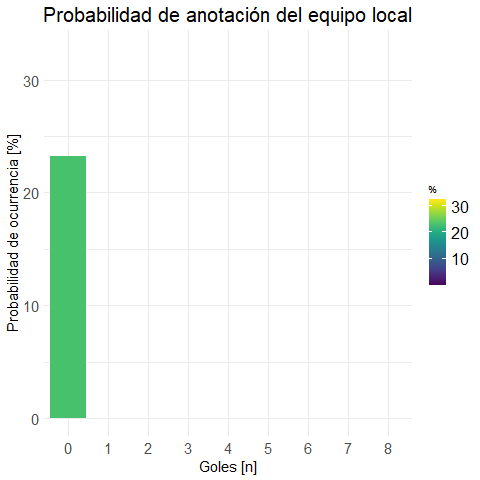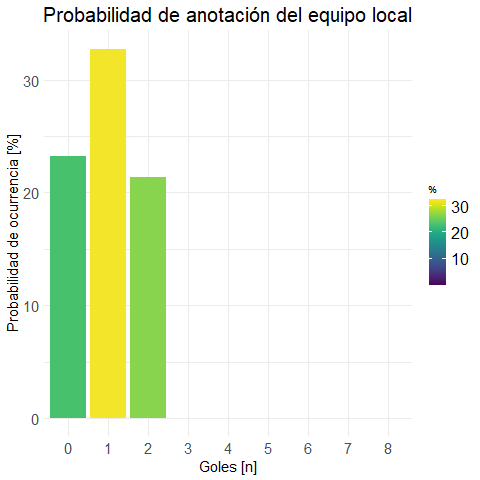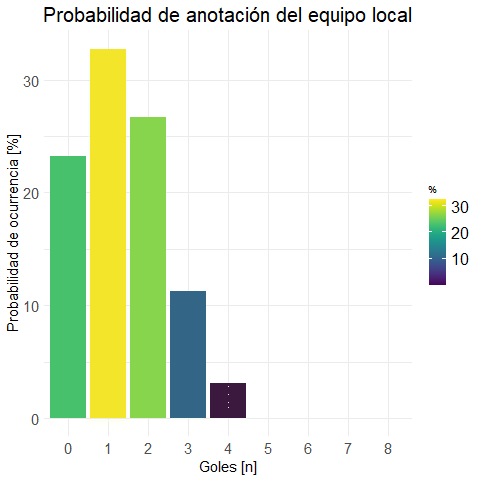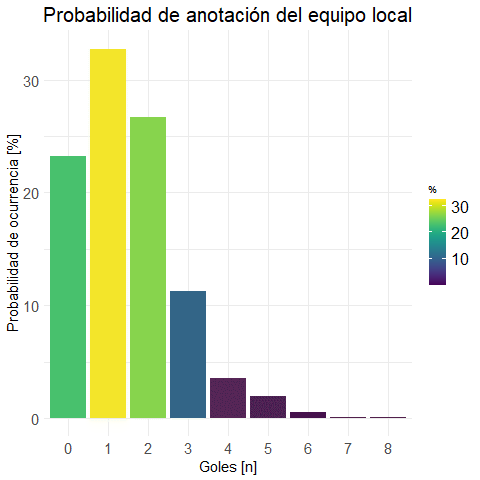
mutate(Date = as.Date(Date, "%Y-%m-%d"))Calcularemos la probabilidad marginal de que el equipo local anote ’x’ goles mediante una función previa:
prob.m.local <-
get.prob.df(data, FTHG, "Gol.Home", "P.Marginal")
(prob.m.local %>% get.round(3))## Gol.Home Freq P.Marginal
## 1 0 265 0.232
## 2 1 373 0.327
## 3 2 304 0.267
## 4 3 128 0.112
## 5 4 40 0.035
## 6 5 22 0.019
## 7 6 6 0.005
## 8 7 1 0.001
## 9 8 1 0.001
Realizamos una función de una gráfica para vizualizar los datos:
plot.bar <- function(data, x.lab, y.lab, f.lab, title){
Goles <- data[1] %>% unlist()
Porcentaje <- (data[3]*100 ) %>% unlist %>% round(., digits=2)
Prob.Marginal <- data[3] %>% unlist() %>% round(., digits=4)
data %>%
ggplot() +
geom_bar(stat = 'identity') +
aes( x = Goles
, y = Porcentaje
, fill = Porcentaje
, text = paste("Prob Marginal", Prob.Marginal)
#, group = interaction(Goles, Porcentaje)
) +
labs( x = x.lab
, y = y.lab
, fill = f.lab
, title = title
) +
theme_minimal() +
theme( text = element_text(size=20)
, legend.title = element_text(size=10)
) +
scale_fill_viridis(name=f.lab, direction = 1) +
theme( axis.text.x = element_text(size = 15) #tamaño de numeros en
, axis.text.y = element_text(size = 15) #tamaño de numeros en y
, axis.title.x = element_text(size = 18) #tamaño del letrero en x
, axis.title.y = element_text(size = 18) #tamaño del letrero en y
, plot.title = element_text(size = 20, hjust = 0.5) #tamaño del titulo
)
}Realizamos una gráfica para vizualizar los datos:
plot.local <- plot.bar(prob.m.local
, "Goles [n]"
, "Probabilidad de ocurrencia [%]"
, "%"
, "Probabilidad de anotación del equipo local"
)ggplotly(plot.local) #versión interactivalibrary(gganimate)
(plot.local.animation <-
plot.local +
transition_states(plot.local$data$Gol.Home, transition_length = 10) +
enter_grow() +
shadow_mark())# Lo generamos como video, para eso es necesario tener ffmpeg instalado:
# Tenerlo descargado y agregar la carpeta Folder_ffmpeg\bin a las variables
# de entorno en Windows
animate(plot.local.animation, duration = 2.7, renderer = ffmpeg_renderer())Ahora calcularemos la probabilidad para el equipo visitante:
prob.m.visit <-
get.prob.df(data, FTAG, "Gol.Away", "P.Marginal")
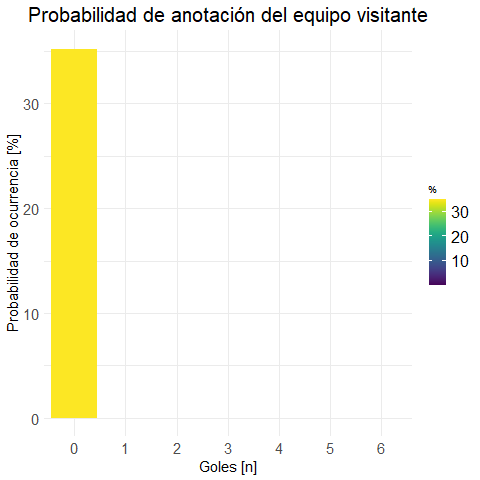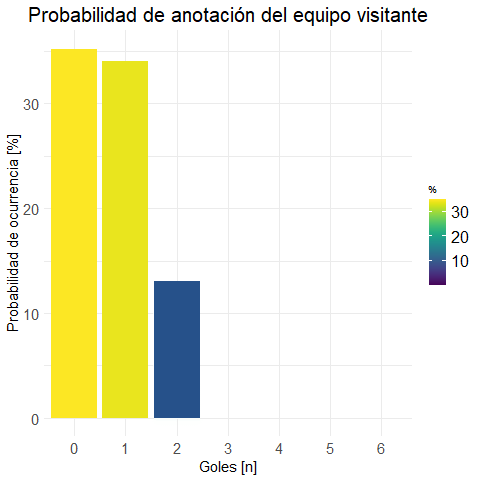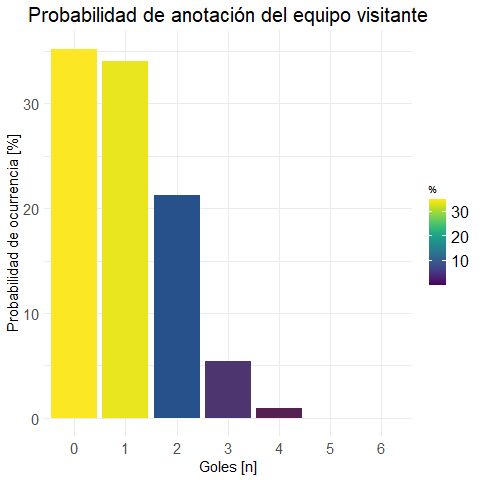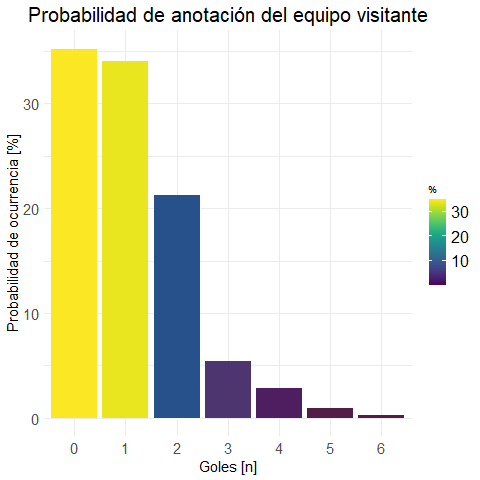
(prob.m.visit %>% get.round(3))## Gol.Away Freq P.Marginal
## 1 0 401 0.352
## 2 1 388 0.340
## 3 2 242 0.212
## 4 3 62 0.054
## 5 4 33 0.029
## 6 5 11 0.010
## 7 6 3 0.003
Realizamos una gráfica para vizualizar los datos:
plot.visit <- plot.bar(prob.m.visit
, "Goles [n]"
, "Probabilidad de ocurrencia [%]"
, "%"
, "Probabilidad de anotación del equipo visitante"
)ggplotly(plot.visit) #versión interactiva(plot.visit.animation <-
plot.visit +
transition_states( plot.visit$data$Gol.Away
, transition_length = 10) +
enter_grow() +
shadow_mark())# Lo generamos como video, para eso es necesario tener ffmpeg instalado:
# Tenerlo descargado y agregar la carpeta Folder_ffmpeg\bin a las variables
# de entorno en Windows
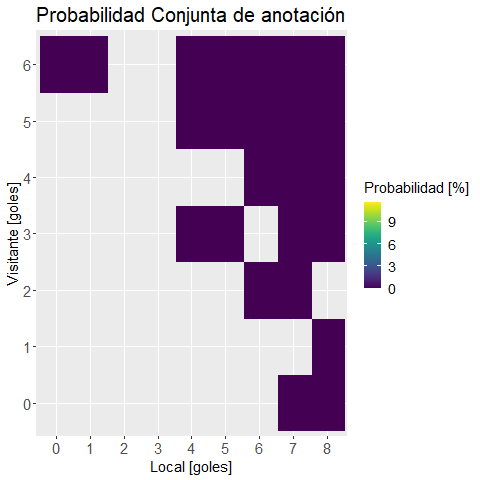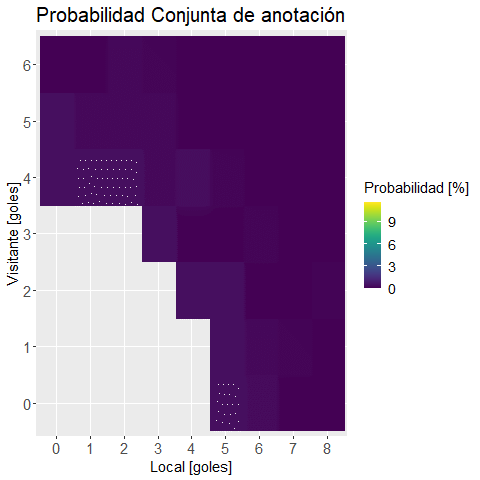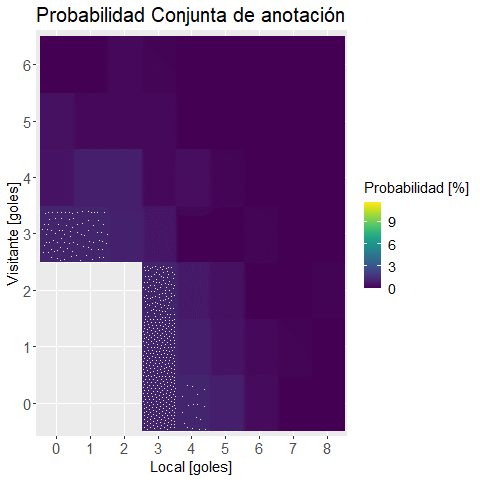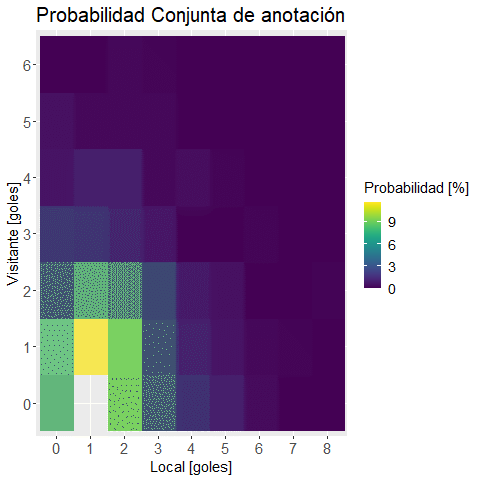
animate(plot.visit.animation, duration = 2.7, renderer = ffmpeg_renderer())La probabilidad conjunta de que el equipo que juega en casa anote ‘x’ goles y el equipo que juega como visitante anote ’y’ goles calculada con una función previa:
prob.joint <-
get.prob.joint.tbl(data, data$FTHG, data$FTAG, "Local", "Visitante")
(prob.joint %<>% "*"(100) %>% round(2))## Visitante
## Local 0 1 2 3 4 5 6
## 0 7.81 8.07 4.56 1.84 0.53 0.44 0.00
## 1 11.58 11.49 6.84 1.75 0.88 0.18 0.00
## 2 8.77 9.39 6.14 1.14 0.88 0.18 0.18
## 3 4.47 3.25 2.46 0.61 0.18 0.18 0.09
## 4 1.40 1.05 0.70 0.00 0.35 0.00 0.00
## 5 0.88 0.53 0.44 0.00 0.09 0.00 0.00
## 6 0.26 0.18 0.00 0.09 0.00 0.00 0.00
## 7 0.00 0.09 0.00 0.00 0.00 0.00 0.00
## 8 0.00 0.00 0.09 0.00 0.00 0.00 0.00
Realizamos un heat map con una función para visualizar los datos:
prob.joint %<>% as.data.frame() %>% rename(Probabilidad = Freq)plot.heatmap <- function(data, x.lab, y.lab, f.lab, title){
Local <- data[1] %>% unlist
Visitante <- data[2] %>% unlist
Probabilidad <- data[3] %>% unlist
ggplot(data) +
aes( Local
, Visitante
, fill = Probabilidad
) + #gráficamos
geom_raster() +
labs( x = x.lab
, y = y.lab
, fill = f.lab
, title = title
) +
theme( text = element_text(size=18)
, legend.title = element_text(size=15)
) +
scale_fill_viridis( name=f.lab
, direction = 1 #, option = "H"
) +
theme( axis.text.x = element_text(size = 15) #tamaño de numeros en
, axis.text.y = element_text(size = 15) #tamaño de numeros en y
, axis.title.x = element_text(size = 18) #tamaño del letrero en x
, axis.title.y = element_text(size = 18) #tamaño del letrero en y
, plot.title = element_text(size = 20, hjust = 0.5) #tamaño del titulo
)
}Realizamos una gráfica para visualizar los datos:
plot.mapa.calor <-
plot.heatmap( prob.joint
, "Local [goles]"
, "Visitante [goles]"
, "Probabilidad [%]"
, "Probabilidad Conjunta de anotación"
)ggplotly(plot.mapa.calor) #versión interactiva(heatmap.animation <-
plot.mapa.calor +
transition_states( plot.mapa.calor$data$Probabilidad/100
, transition_length = 20) +
enter_grow() +
shadow_mark())# Lo generamos como video, para eso es necesario tener ffmpeg instalado:
# Tenerlo descargado y agregar la carpeta Folder_ffmpeg\bin a las variables
# de entorno en Windows
animate(heatmap.animation, duration = 7, renderer = ffmpeg_renderer())Ahora obtendremos una tabla de cocientes al dividir las probabilidades conjuntas por el producto de las probabilidades correspondientes:
Cocientes = P(x∩y)/(P(x) * P(y))
data <- read.csv("https://raw.githubusercontent.com/napoleonleal/R-BEDU-Project/main/Postwork_2/Postwork_02.csv")Para la probabilidad marginal de los goles metidos por locales con una función previa:
prob.m.local <- get.prob.df(data, FTHG, "Gol.Home", "Prob.Marginal")
(prob.m.local %>% get.round(3))## Gol.Home Freq Prob.Marginal
## 1 0 363 0.239
## 2 1 503 0.331
## 3 2 402 0.264
## 4 3 157 0.103
## 5 4 59 0.039
## 6 5 27 0.018
## 7 6 7 0.005
## 8 7 1 0.001
## 9 8 1 0.001
Para los goles metidos por el equipo visitante:
prob.m.visit <- get.prob.df(data, FTAG, "Gol.Away", "Prob.Marginal")
(prob.m.visit %>% get.round(3))## Gol.Away Freq Prob.Marginal
## 1 0 516 0.339
## 2 1 540 0.355
## 3 2 315 0.207
## 4 3 90 0.059
## 5 4 43 0.028
## 6 5 12 0.008
## 7 6 4 0.003
Hacemos el producto de las probabilidades marginales obtenidas con una función previa:
tbl.local <- get.prob.m.tbl(data, FTHG, "Home")
tbl.visit <- get.prob.m.tbl(data, FTAG, "Away")
product.prob.m <- tbl.local %o% tbl.visit
(product.prob.m %>% round(3))## Away
## Home 0 1 2 3 4 5 6
## 0 0.081 0.085 0.049 0.014 0.007 0.002 0.001
## 1 0.112 0.118 0.069 0.020 0.009 0.003 0.001
## 2 0.090 0.094 0.055 0.016 0.007 0.002 0.001
## 3 0.035 0.037 0.021 0.006 0.003 0.001 0.000
## 4 0.013 0.014 0.008 0.002 0.001 0.000 0.000
## 5 0.006 0.006 0.004 0.001 0.001 0.000 0.000
## 6 0.002 0.002 0.001 0.000 0.000 0.000 0.000
## 7 0.000 0.000 0.000 0.000 0.000 0.000 0.000
## 8 0.000 0.000 0.000 0.000 0.000 0.000 0.000
Obtenemos la probabilidad conjunta con una función previa:
prob.conjunta <-
get.prob.joint.tbl(data, data$FTHG, data$FTAG, "Home", "Away")
(prob.conjunta %>% round(3))## Away
## Home 0 1 2 3 4 5 6
## 0 0.078 0.083 0.051 0.018 0.006 0.003 0.000
## 1 0.112 0.123 0.062 0.022 0.009 0.002 0.001
## 2 0.086 0.097 0.060 0.012 0.008 0.001 0.001
## 3 0.039 0.032 0.022 0.006 0.003 0.001 0.001
## 4 0.015 0.013 0.007 0.001 0.003 0.000 0.000
## 5 0.007 0.005 0.005 0.000 0.001 0.000 0.000
## 6 0.002 0.002 0.000 0.001 0.000 0.000 0.000
## 7 0.000 0.001 0.000 0.000 0.000 0.000 0.000
## 8 0.000 0.000 0.001 0.000 0.000 0.000 0.000
Realizamos el cociente:
cociente <- prob.conjunta/product.prob.m
(cociente %>% round(2))## Away
## Home 0 1 2 3 4 5 6
## 0 0.97 0.98 1.02 1.26 0.88 1.74 0.00
## 1 1.00 1.05 0.91 1.14 0.91 0.76 0.76
## 2 0.95 1.03 1.09 0.76 1.06 0.63 1.89
## 3 1.13 0.86 1.01 0.97 0.90 1.61 2.42
## 4 1.15 0.95 0.90 0.29 2.40 0.00 0.00
## 5 1.20 0.83 1.25 0.00 1.31 0.00 0.00
## 6 1.26 1.21 0.00 2.41 0.00 0.00 0.00
## 7 0.00 2.81 0.00 0.00 0.00 0.00 0.00
## 8 0.00 0.00 4.83 0.00 0.00 0.00 0.00
Para determinar si el número de goles del equipo local o el de el equipo visitante son dependientes o independientes, realizaremos un procedimiento de bootstrap para obtener más cocientes similares y analizar la distribución.
Transformamos el data frame a columna para facilitar el bootstrap.
data_origin <- as.data.frame(as.vector(unlist(cociente)))
colnames(data_origin) <- "values"Utilizamos la biblioteca "rsample" para poder hacer las muestras
bootstrap:
library(rsample)Fijamos la semilla para poder reproducir los datos:
set.seed(83928782)Aplicamos la función bootstraps, para generar 1000 muestras, guardándolas en boot:
boot <- bootstraps(data_origin, times = 1000)Cargamos las siguientes bibliotecas para visualizar datos:
library(purrr)
library(modeldata)
library(viridis)
library(tidyverse)
library(hrbrthemes)
library(forcats)
library(viridisLite)Realizamos una función para hacer una columna de las medias muestrales obtenidas por bootstrap:
obtener_media <- function(boot_splits) {
data_mean <- analysis(boot_splits)
medias_muestrales <- mean(data_mean[,1])
return(medias_muestrales)
}Observamos el valor de la media de las medias muestrales tras aplicar la función:
boot$means <- map_dbl(boot$splits, obtener_media)
length(boot$means); summary(boot$means)## [1] 1000
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.4996 0.7523 0.8256 0.8288 0.9048 1.1796
Comprobamos la hipótesis de que la media se encuentra en 1 con las medias muestrales bootstrap y obtenemos el intervalo de confianza al 95% con una prueba t:
t_boot <- t.test(boot$means, alternative = "two.sided", mu = 1)
t_boot_ic <- round(t_boot$conf.int,3)
t_boot_ic## [1] 0.822 0.835
## attr(,"conf.level")
## [1] 0.95
Realizamos una función para un histograma:
plot.histogram <- function( data, data_mean, ic_2, n_bins
, title, x.lab, y.lab, f.lab ){
ggplot(data) +
geom_histogram( bins = n_bins
, color=NA
, aes(fill=..count..)
) +
aes(data_mean) +
labs( x = x.lab
, y = y.lab
, fill = f.lab
, title = title
) +
geom_vline(
aes( xintercept = mean(data_mean))
) +
geom_vline( xintercept = c(ic_2), ####
linetype = c(2,2)
) +
scale_fill_viridis(name = f.lab) +
theme_minimal() +
#theme_ipsum() +
theme( text = element_text(size=18)
, legend.title = element_text(size=15)
, panel.spacing = unit(0.1, "lines")
, strip.text.x = element_text(size = 10)
#legend.position="none",
)
}Realizamos el histograma de las medias muestrales obtenidas por bootstrap.
ic_mean_ic <- c(t_boot_ic[1],
mean(boot$means),
t_boot_ic[2])
hist_boot <-
plot.histogram( boot
, boot$means
, t_boot_ic
, 18
, paste("Histograma de las medias muestrales bootstrap"
, "\n<i><b>n="
, length(boot$means)
, "</b></i>"
, sep = ""
)
, "Valor de la Media"
, "Frecuencia"
, "Frec"
)ggplotly(hist_boot)La línea sólida indica la posición de la media y las punteadas, la posición de los límites del intervalo de confianza.
De igual modo lo hacemos para la muestra original:
t_origin <- t.test(data_origin$values, alternative = "two.sided", mu = 1)
t_origin_ic <- t_origin$conf.int %>% round(3)
t_origin_ic## [1] 0.613 1.053
## attr(,"conf.level")
## [1] 0.95
ori_ic_mean_ic <- c(t_origin_ic[1],
mean(data_origin$values),
t_origin_ic[2])
hist_origin <-
plot.histogram( data_origin
, data_origin$values
, t_origin_ic
, 11
, "Histograma de la muestra original"
, "Valor de la Muestra"
, "Frecuencia"
, "Frec"
)ggplotly(hist_origin)La línea sólida indica la posición de la media y las punteadas, la posición de los límites del intervalo de confianza.
Vemos los datos de los estadísticos de las pruebas t para ambos conjuntos de datos.
Remuestreo bootstrap:
t_boot##
## One Sample t-test
##
## data: boot$means
## t = -50.464, df = 999, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 1
## 95 percent confidence interval:
## 0.8221057 0.8354231
## sample estimates:
## mean of x
## 0.8287644
Muestras originales:
t_origin##
## One Sample t-test
##
## data: data_origin$values
## t = -1.5194, df = 62, p-value = 0.1338
## alternative hypothesis: true mean is not equal to 1
## 95 percent confidence interval:
## 0.6130959 1.0527411
## sample estimates:
## mean of x
## 0.8329185
Observamos como la distribución de la media de los cocientes no era normal. Usamos la media muestral de 1000 muestras generadas por método bootstrap y acorde al Teorema del Límite Central observamos que la distribución de las medias muestrales bootstrap es normal.
Por medio de una prueba de hipótesis y los intervalos de confianza vimos que no hay evidencia significativa para establecer que la media de los cocientes tienda a 1. Por tanto, podemos considerar a las variables como dependientes.
Con los datos de la liga de primera división española, de las temporadas 2017/2018, 2018/2019 y 2019/2020 haremos una predicción de los resultados de los partidos de la fecha 07/16/2020.
Utilizamos la librería dplyr para manipulaciín de datos:
library(dplyr)Y la librería fbRanks para las predicciones en base al modelo de Dixon y Coles:
library(fbRanks)Guardamos los datos de las 3 temporadas en una lista. Seleccionamos unicamente los elementos “Date”, “HomeTeam”, “FTHG”, “AwayTeam” ,“FTAG”, los cuales son esenciales para el modelo y cambiamos los nombres de las columnas por requerimiento de la biblioteca. Unimos las 3 temporadas en una sola y Cambiamos la forma del año, para poder aplicar un único formato date:
columns <- c( date = "Date"
, home.team = "HomeTeam"
, away.team = "AwayTeam"
, home.score = "FTHG"
, away.score = "FTAG"
)
SmallData <-
c( "https://www.football-data.co.uk/mmz4281/1718/SP1.csv"
, "https://www.football-data.co.uk/mmz4281/1819/SP1.csv"
, "https://www.football-data.co.uk/mmz4281/1920/SP1.csv"
) %>%
lapply (read.csv) %>%
lapply (select, all_of(columns)) %>%
do.call(rbind, .) %>%
mutate (date = gsub("/(1[78])$",
"/20\\1", date)) %>%
mutate (date = as.Date(date, "%d/%m/%Y"))Guardamos los cambios en un archivo csv:
w.dir <- getwd()
sub.dir <- "equipo10"
path <- file.path(w.dir, sub.dir)
dir.create(path, showWarnings = F, recursive = T)
setwd(path)
write.csv(SmallData, file = './soccer.csv', row.names = F)
setwd(w.dir)Aplicamos la primera función de la biblioteca, “create.fbranks.dataframes” con la finalidad de poder hacer una limpieza de datos, excluyendo los datos nulos para las puntuaciones, así como nombres repetidos, los cambios incluyen la transformación del formato de columna “date”:
listasoccer <- create.fbRanks.dataframes(scores.file = "soccer.csv")## Alert: teams info file was not passed in.
## Will construct one from the scores data frame but teams in the scores file must use a unique name.
## Alert: teams resolver was not passed in.
## Will construct one from the team info data frame.
(listasoccer)## $scores
## date home.team away.team home.score away.score
## 1 2017-08-18 Leganes Alaves 1 0
## 2 2017-08-18 Valencia Las Palmas 1 0
## 3 2017-08-19 Celta Sociedad 2 3
## 4 2017-08-19 Girona Ath Madrid 2 2
## 5 2017-08-19 Sevilla Espanol 1 1
## 6 2017-08-20 Ath Bilbao Getafe 0 0
## 7 2017-08-20 Barcelona Betis 2 0
## 8 2017-08-20 La Coruna Real Madrid 0 3
...
Como residuo, la función nos devuelve una lista con un data.frame scores con los datos de nuestro csv limpios y las fechas en orden ascendente, como también el data frame teams, en este caso generado del csv, con los nombres de los equipos sin repetir, el data.frame teams.resolver y por último el data.frame raw.scores, con algunas configuraciones para el uso de otras funciones.
View(listasoccer)Guardamos el data.frame scores generados, con las puntuaciones en las temporadas
anotaciones = listasoccer$scoresGuardamos la lista de equipos
equipos = listasoccer$teamsGuardamos las fechas sin repetir
fecha = unique(listasoccer$scores$date)Y la cantidad de las fechas para un mejor control
n = length(fecha)Aplicamos la función “rank.teams”, el cual aplica una regresión lineal usando como modelo la distribución de Poisson, tomando como rango de tiempo la duración de un partido.
La función requiere los datos scores, la lista de equipos y las fechas entre las que generamos nuestro ranking
ranking = rank.teams( anotaciones
, equipos
, max.date = fecha[n-1]
, min.date = fecha[1]
, date.format = "%Y-%m-%d")##
## Team Rankings based on matches 2017-08-18 to 2020-07-16
## team total attack defense n.games.Var1 n.games.Freq
## 1 Barcelona 1.51 2.23 1.28 Barcelona 113
## 2 Ath Madrid 1.24 1.33 1.78 Ath Madrid 113
## 3 Real Madrid 1.15 1.86 1.19 Real Madrid 113
## 4 Valencia 0.56 1.34 1.10 Valencia 113
## 5 Getafe 0.55 1.10 1.33 Getafe 113
## 6 Sevilla 0.43 1.37 0.98 Sevilla 113
## 7 Granada 0.37 1.26 1.03 Granada 37
...
Como resultado nos da una lista con las especificaciones que le dimos a nuestra función Y nos presenta una tabla ranking, con los coeficientes de la regresión, tanto de ataque y defensa, modificados para su mejor comprensión, y uniéndolos en un total, posicionando a los equipos con base en el total.
(ranking)##
## Team Rankings based on matches 2017-08-18 to 2020-07-16
## team total attack defense n.games.Var1 n.games.Freq
## 1 Barcelona 1.51 2.23 1.28 Barcelona 113
## 2 Ath Madrid 1.24 1.33 1.78 Ath Madrid 113
## 3 Real Madrid 1.15 1.86 1.19 Real Madrid 113
## 4 Valencia 0.56 1.34 1.10 Valencia 113
## 5 Getafe 0.55 1.10 1.33 Getafe 113
## 6 Sevilla 0.43 1.37 0.98 Sevilla 113
## 7 Granada 0.37 1.26 1.03 Granada 37
...
La función da como resultado una clase única de la librería “fbRanks” necesaria para el uso de otras funciones
class(ranking)## [1] "fbRanks"
En la lista “ranking” es posible encontrar los coeficientes de la regresión en crudo, como sus especificaciones
ranking[1]## $fit
## $fit$cluster.1
##
## Call: glm(formula = as.formula(my.formula), family = family, weights = exp(-1 *
## time.weight.eta * time.diff), na.action = "na.exclude")
##
## Coefficients:
## attackAlaves attackAth Bilbao attackAth Madrid attackBarcelona
## 0.0494074 0.1262803 0.3912525 0.9066502
## attackBetis attackCelta attackEibar attackEspanol
...
View(ranking[1])Podemos extraer los datos de la función rank
columns = c( team = "ranks.team"
, total = "ranks.total"
, attack = "ranks.attack"
, defense = "ranks.defense"
, n.games.Var1 = "ranks.n.games.Var1"
, n.games.Freq = "ranks.n.games.Freq"
)
Ranking.datos <-
ranking %>%
print %>%
as.data.frame %>%
select(all_of(columns))##
## Team Rankings based on matches 2017-08-18 to 2020-07-16
## team total attack defense n.games.Var1 n.games.Freq
## 1 Barcelona 1.51 2.23 1.28 Barcelona 113
## 2 Ath Madrid 1.24 1.33 1.78 Ath Madrid 113
## 3 Real Madrid 1.15 1.86 1.19 Real Madrid 113
## 4 Valencia 0.56 1.34 1.10 Valencia 113
## 5 Getafe 0.55 1.10 1.33 Getafe 113
## 6 Sevilla 0.43 1.37 0.98 Sevilla 113
## 7 Granada 0.37 1.26 1.03 Granada 37
...
y aprovecharlos para hacer diversos análisis teniéndolos en formato csv ya exportado podemos tomarlo del link de nuestro repositorio:
Ranking.datos <- read.csv("https://raw.githubusercontent.com/napoleonleal/R-BEDU-Project/main/ranking20.csv")Basándonos en nuestro modelo, podemos ver el máximo atacante, y el máximo defensor
(Max.atacante <- Ranking.datos %>% filter(attack == max(attack)))## team total attack defense n.games.Var1 n.games.Freq
## 1 Barcelona 1.51 2.23 1.28 Barcelona 113
(Max.defensor <- Ranking.datos %>% filter(defense == max(defense)))## team total attack defense n.games.Var1 n.games.Freq
## 1 Ath Madrid 1.24 1.33 1.78 Ath Madrid 113
Como también el resumen
summary(Ranking.datos)## team total attack defense
## Length:26 Min. :-1.43000 Min. :0.5800 Min. :0.6000
## Class :character 1st Qu.:-0.32500 1st Qu.:0.9675 1st Qu.:0.7875
## Mode :character Median : 0.00000 Median :1.0950 Median :0.9050
## Mean : 0.02885 Mean :1.1600 Mean :0.9442
## 3rd Qu.: 0.36000 3rd Qu.:1.3175 3rd Qu.:1.0225
## Max. : 1.51000 Max. :2.2300 Max. :1.7800
##
## n.games.Var1 n.games.Freq
## Barcelona : 1 Min. : 37.00
...
Para las predicciones referentes a los últimos partidos de la liga, utilizaremos la función “predict”, que se basa en el modelo de Dixon and Coles, el cual es una modificación del modelo de predicciones de distribuciones de Poisson, con una modificación en cuanto a la sobre-estimación de los datos fuera de la media.
La función requiere un objeto clase “fbRank”, ya que hace uso de los coeficientes de la regresión lineal.
prediccion = predict.fbRanks(ranking, date = fecha[n])## Predicted Match Results for 1900-05-01 to 2100-06-01
## Model based on data from 2017-08-18 to 2020-07-16
## ---------------------------------------------
## 2020-07-19 Alaves vs Barcelona, HW 9%, AW 76%, T 16%, pred score 0.7-2.5 actual: AW (0-5)
## 2020-07-19 Valladolid vs Betis, HW 29%, AW 43%, T 28%, pred score 1-1.3 actual: HW (2-0)
## 2020-07-19 Villarreal vs Eibar, HW 45%, AW 30%, T 25%, pred score 1.5-1.2 actual: HW (4-0)
## 2020-07-19 Ath Madrid vs Sociedad, HW 54%, AW 20%, T 26%, pred score 1.5-0.8 actual: T (1-1)
## 2020-07-19 Espanol vs Celta, HW 32%, AW 41%, T 27%, pred score 1.2-1.4 actual: T (0-0)
## 2020-07-19 Granada vs Ath Bilbao, HW 40%, AW 31%, T 29%, pred score 1.2-1 actual: HW (4-0)
## 2020-07-19 Leganes vs Real Madrid, HW 13%, AW 66%, T 21%, pred score 0.7-1.9 actual: T (2-2)
...
La función regresa una lista, con data.frames y vectores, nos enfocaremos principalmente en su primer objeto “scores”, a diferencia de nuestro csv, solo contiene los datos sobre los últimos partidos, dando como información las probabilidades de victoria, derrota, empate victoria-derrota con 0 goles del rival, ademas de incluir los coeficientes de la regresión
View(prediccion[1])Centrándonos en las probabilidades de victoria, derrota, empate para el equipo de local como también la predicción del número de goles redondeada:
columns <-
c( Home.team = "home.team"
, Away.team = "away.team"
, Prob.win.home = "home.win"
, Prob.win.away = "away.win"
, Prob.tie = "tie"
, Pred.home.score = "pred.home.score"
, Pred.away.score = "pred.away.score"
)
predict.prob <-
prediccion$scores %>% as.data.frame %>% select(all_of(columns)) %>%
mutate( Pred.home.score = Pred.home.score %>% round(0)
, Pred.away.score = Pred.away.score %>% round(0))
(predict.prob)## Home.team Away.team Prob.win.home Prob.win.away Prob.tie
## 1131 Alaves Barcelona 8.814 75.668 15.518
## 1132 Valladolid Betis 28.672 43.066 28.262
## 1133 Villarreal Eibar 44.932 29.754 25.314
## 1134 Ath Madrid Sociedad 53.669 19.958 26.373
## 1135 Espanol Celta 31.949 41.429 26.622
## 1136 Granada Ath Bilbao 39.629 31.135 29.236
## 1137 Leganes Real Madrid 12.720 66.207 21.073
## 1138 Levante Getafe 25.172 47.890 26.938
## 1139 Osasuna Mallorca 47.992 27.228 24.780
...
Hacemos una comparación con los datos reales:
columns <-
c( Home.team = "home.team"
, Home.score = "home.score"
, Pred.home.score = "pred.home.score"
, Away.team = "away.team"
, Away.score = "away.score"
, Pred.away.score = "pred.away.score"
)
comparacion <-
prediccion$scores %>% as.data.frame %>% select(all_of(columns)) %>%
mutate( Pred.home.score = Pred.home.score %>% round(0)
, Pred.away.score = Pred.away.score %>% round(0))Los partidos en los cuales acertó el número de goles del equipo de local
(comparacion %>% filter(Home.score == Pred.home.score))## Home.team Home.score Pred.home.score Away.team Away.score Pred.away.score
## 1 Ath Madrid 1 1 Sociedad 1 1
## 2 Levante 1 1 Getafe 0 1
## 3 Osasuna 2 2 Mallorca 2 1
## 4 Sevilla 1 1 Valencia 0 1
Y en donde acertó los goles del equipo visitante
(comparacion %>% filter(Away.score == Pred.away.score))## Home.team Home.score Pred.home.score Away.team Away.score Pred.away.score
## 1 Ath Madrid 1 1 Sociedad 1 1
## 2 Leganes 2 1 Real Madrid 2 2
Hacemos la predicción de todas las fechas de los partidos usando el objeto ranking y obtenemos la matriz de confusión donde las clases son el número de goles
prediccion.total.partidos = predict.fbRanks(ranking, date = fecha)## Predicted Match Results for 1900-05-01 to 2100-06-01
## Model based on data from 2017-08-18 to 2020-07-16
## ---------------------------------------------
## 2017-08-18 Leganes vs Alaves, HW 33%, AW 35%, T 32%, pred score 0.9-1 actual: HW (1-0)
## 2017-08-18 Valencia vs Las Palmas, HW 75%, AW 8%, T 17%, pred score 2.1-0.5 actual: HW (1-0)
## 2017-08-19 Celta vs Sociedad, HW 32%, AW 45%, T 23%, pred score 1.4-1.7 actual: AW (2-3)
## 2017-08-19 Girona vs Ath Madrid, HW 14%, AW 62%, T 25%, pred score 0.6-1.6 actual: T (2-2)
## 2017-08-19 Sevilla vs Espanol, HW 49%, AW 24%, T 26%, pred score 1.5-0.9 actual: T (1-1)
## 2017-08-20 Ath Bilbao vs Getafe, HW 27%, AW 40%, T 33%, pred score 0.8-1 actual: T (0-0)
## 2017-08-20 Barcelona vs Betis, HW 74%, AW 11%, T 15%, pred score 2.8-1 actual: HW (2-0)
...
columns <-
c( Home.team = "home.team"
, Home.score = "home.score"
, Pred.home.score = "pred.home.score"
, Away.team = "away.team"
, Away.score = "away.score"
, Pred.away.score = "pred.away.score"
)
comparacion.total.partidos <-
prediccion.total.partidos$scores %>% as.data.frame %>% select(all_of(columns)) %>%
mutate( Pred.home.score = Pred.home.score %>% round(0)
, Pred.away.score = Pred.away.score %>% round(0))library(caret)
library(lattice)confusion.m.local <-
confusionMatrix( factor( comparacion.total.partidos$Pred.home.score
, levels = 0:max(comparacion.total.partidos$Home.score))
, factor( comparacion.total.partidos$Home.score
, levels = 0:max(comparacion.total.partidos$Home.score))
, dnn = c("Prediccion", "Valores Reales"))
(confusion.m.local)## Confusion Matrix and Statistics
##
## Valores Reales
## Prediccion 0 1 2 3 4 5 6 7 8
## 0 8 4 1 0 0 0 0 0 0
## 1 226 305 210 78 19 4 1 0 0
## 2 31 61 86 44 19 16 4 0 0
## 3 0 3 7 5 1 2 1 1 1
## 4 0 0 0 1 1 0 0 0 0
## 5 0 0 0 0 0 0 0 0 0
## 6 0 0 0 0 0 0 0 0 0
## 7 0 0 0 0 0 0 0 0 0
## 8 0 0 0 0 0 0 0 0 0
##
## Overall Statistics
##
## Accuracy : 0.3553
## 95% CI : (0.3274, 0.3838)
## No Information Rate : 0.3272
## P-Value [Acc > NIR] : 0.02395
##
## Kappa : 0.0686
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5
## Sensitivity 0.030189 0.8177 0.28289 0.039062 0.0250000 0.0000
## Specificity 0.994286 0.2986 0.79067 0.984190 0.9990909 1.0000
## Pos Pred Value 0.615385 0.3618 0.32950 0.238095 0.5000000 NaN
## Neg Pred Value 0.771961 0.7710 0.75199 0.890080 0.9657293 0.9807
## Prevalence 0.232456 0.3272 0.26667 0.112281 0.0350877 0.0193
## Detection Rate 0.007018 0.2675 0.07544 0.004386 0.0008772 0.0000
## Detection Prevalence 0.011404 0.7395 0.22895 0.018421 0.0017544 0.0000
## Balanced Accuracy 0.512237 0.5581 0.53678 0.511626 0.5120455 0.5000
## Class: 6 Class: 7 Class: 8
## Sensitivity 0.000000 0.0000000 0.0000000
## Specificity 1.000000 1.0000000 1.0000000
## Pos Pred Value NaN NaN NaN
## Neg Pred Value 0.994737 0.9991228 0.9991228
## Prevalence 0.005263 0.0008772 0.0008772
## Detection Rate 0.000000 0.0000000 0.0000000
## Detection Prevalence 0.000000 0.0000000 0.0000000
## Balanced Accuracy 0.500000 0.5000000 0.5000000
Vemos que la exactitud (accuracy), que es la cantidad de predicciones positivas que fueron correctas y que esta dada por la suma de la diagonal entre la suma total, es de 35.53%. El modelo acertó en el 35.53% de su predicción.
Además se aprecia la relación entre los valores predecidos y los reales.
En la sensibilidad (sensitivity), que es la proporción de casos positivos que fueron correctamente identificados, vemos que el valor más alto es cuando predice que el equipo local anota 1 gol. El modelo acertó en el 81.77% de las anotaciones reales que fueron de 1 gol.
Al ver la distribución de la matriz notamos que el modelo no acertó la predicción en ningún valor de 5 a 8 goles. Ni siquiera hubo esos valores en su predicción.
Y el “Pos Pred Value” es la proporción de predicciones correctamente identificadas del total de predicciones para cada clase. De todos los marcadores con gol 0 que predijo, el 61.53% fue acertado. Los demas están por abajo del 50%.
confusion.m.visit <-
confusionMatrix( factor( comparacion.total.partidos$Pred.away.score
, levels = 0:max(comparacion.total.partidos$Away.score)
)
, factor( comparacion.total.partidos$Away.score
, levels = 0:max(comparacion.total.partidos$Away.score))
, dnn = c("Prediccion", "Valores Reales"))
(confusion.m.visit)## Confusion Matrix and Statistics
##
## Valores Reales
## Prediccion 0 1 2 3 4 5 6
## 0 12 0 1 0 0 0 0
## 1 336 299 155 39 10 4 0
## 2 49 86 81 18 19 5 3
## 3 4 2 5 5 3 2 0
## 4 0 1 0 0 1 0 0
## 5 0 0 0 0 0 0 0
## 6 0 0 0 0 0 0 0
##
## Overall Statistics
##
## Accuracy : 0.3491
## 95% CI : (0.3214, 0.3776)
## No Information Rate : 0.3518
## P-Value [Acc > NIR] : 0.5848
##
## Kappa : 0.063
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5
## Sensitivity 0.02993 0.7706 0.33471 0.080645 0.0303030 0.000000
## Specificity 0.99865 0.2766 0.79955 0.985158 0.9990967 1.000000
## Pos Pred Value 0.92308 0.3547 0.31034 0.238095 0.5000000 NaN
## Neg Pred Value 0.65484 0.7003 0.81684 0.949062 0.9718805 0.990351
## Prevalence 0.35175 0.3404 0.21228 0.054386 0.0289474 0.009649
## Detection Rate 0.01053 0.2623 0.07105 0.004386 0.0008772 0.000000
## Detection Prevalence 0.01140 0.7395 0.22895 0.018421 0.0017544 0.000000
## Balanced Accuracy 0.51429 0.5236 0.56713 0.532901 0.5146998 0.500000
## Class: 6
## Sensitivity 0.000000
## Specificity 1.000000
## Pos Pred Value NaN
## Neg Pred Value 0.997368
## Prevalence 0.002632
## Detection Rate 0.000000
## Detection Prevalence 0.000000
## Balanced Accuracy 0.500000
Vemos que la exactitud (accuracy), que es la cantidad de predicciones positivas que fueron correctas y que esta dada por la suma de la diagonal entre la suma total, es de 35.53%. El modelo acertó en el 35.53% de su predicción.
Además se aprecia la relación entre los valores predecidos y los reales.
En la sensibilidad (sensitivity), que es la proporción de casos positivos que fueron correctamente identificados, vemos que el valor más alto es cuando predice que el equipo local anota 1 gol. El modelo acertó en el 81.77% de las anotaciones reales que fueron de 1 gol.
Al ver la distribución de la matriz notamos que el modelo no acertó la predicción en ningún valor de 5 a 8 goles. Ni siquiera hubo esos valores en su predicción.
Y el "Pos Pred Value" es la proporción de predicciones correctamente identificadas del total de predicciones para cada clase. De todos los marcadores con gol cero que predijo, el 61.53% fue acertado. Los demás están por abajo del 50%.
En las últimas comparaciones de las predicciones hechas por la librería fbRanks podemos notar que la predicción en cuanto el número de goles debe tomarse con mucho cuidado, esto ya que por ejemplo en el partido jugado por Barcelona, en el partido éste anotó 5 goles, estos casos son muy poco probables, más si es usado el modelo de Dixon y Coles, ya que reduce la posible sobre-estimación de estos casos, debido a su rareza, de 10 partidos acertó totalmente en 1 partido, por lo que estos análisis pueden servir como referencia, pero la predicción de resultados de juegos puede ser muy compleja, por el número de factores involucrados.
En las métricas obtenidas por la matriz de confusión de la predicción para todas las fechas con las que trabajamos obtuvimos un acierto aproximado de 35% tanto para las predicciones de los goles de casa como visitante.
Importamos el conjunto de datos match.data.csv a R:
df <- read.csv("https://raw.githubusercontent.com/beduExpert/Programacion-R-Santander-2021/main/Sesion-06/Postwork/match.data.csv")
head(df)## date home.team home.score away.team away.score
## 1 2010-08-28 Hercules 0 Ath Bilbao 1
## 2 2010-08-28 Levante 1 Sevilla 4
## 3 2010-08-28 Malaga 1 Valencia 3
## 4 2010-08-29 Espanol 3 Getafe 1
## 5 2010-08-29 La Coruna 0 Zaragoza 0
## 6 2010-08-29 Mallorca 0 Real Madrid 0
summary(df)## date home.team home.score away.team
## Length:3800 Length:3800 Min. : 0.000 Length:3800
## Class :character Class :character 1st Qu.: 1.000 Class :character
## Mode :character Mode :character Median : 1.000 Mode :character
## Mean : 1.589
## 3rd Qu.: 2.000
## Max. :10.000
## away.score
## Min. :0.000
## 1st Qu.:0.000
...
Agregamos una nueva columna "sumagoles" que contiene la suma de goles por partido.
df["sumagoles"] <- df$home.score+df$away.scoreObtuvimos el promedio por mes de la columna suma de goles. Revisamos el tipo de dato de la fecha
class(df$date)## [1] "character"
df$date <- as.Date(df$date)
class(df$date)## [1] "Date"
df$fecha <- format(df$date, format = "%Y-%m")
golesxmes <- aggregate( df$sumagoles ~ df$fecha, df , mean)
View(golesxmes)Creamos la serie de tiempo del promedio por mes de la suma de goles hasta diciembre de 2019.
golesxmes.ts <- ts(golesxmes[ ,2], start = c(2010,08), end = c(2019,12), frequency = 10)
golesxmes.ts## Time Series:
## Start = c(2010, 8)
## End = c(2020, 2)
## Frequency = 10
## [1] 2.200000 2.425000 3.025641 2.902439 2.733333 3.000000 2.325000 2.400000
## [9] 2.930233 2.957447 3.000000 2.525000 2.420000 2.833333 2.900000 2.550000
## [17] 3.050000 2.981818 2.854545 2.700000 3.000000 2.871795 2.838710 2.829268
## [25] 2.794872 3.025000 2.750000 2.657895 3.023810 2.725000 3.800000 2.920000
## [33] 2.711111 2.850000 3.166667 3.125000 2.902439 2.500000 2.474576 2.769231
## [41] 2.387097 2.400000 2.650000 2.903226 2.631579 2.400000 2.555556 2.780488
...
plot(golesxmes.ts, xlab = "Tiempo", ylab = "Promedio de goles", type = "o",
pch = 12, col = "black", lwd = 2, cex = 2) + #Grafica de la serie de tiempo
title(main = "Serie de tiempo", sub = "Frecuencia = 10", cex.sub = 1,
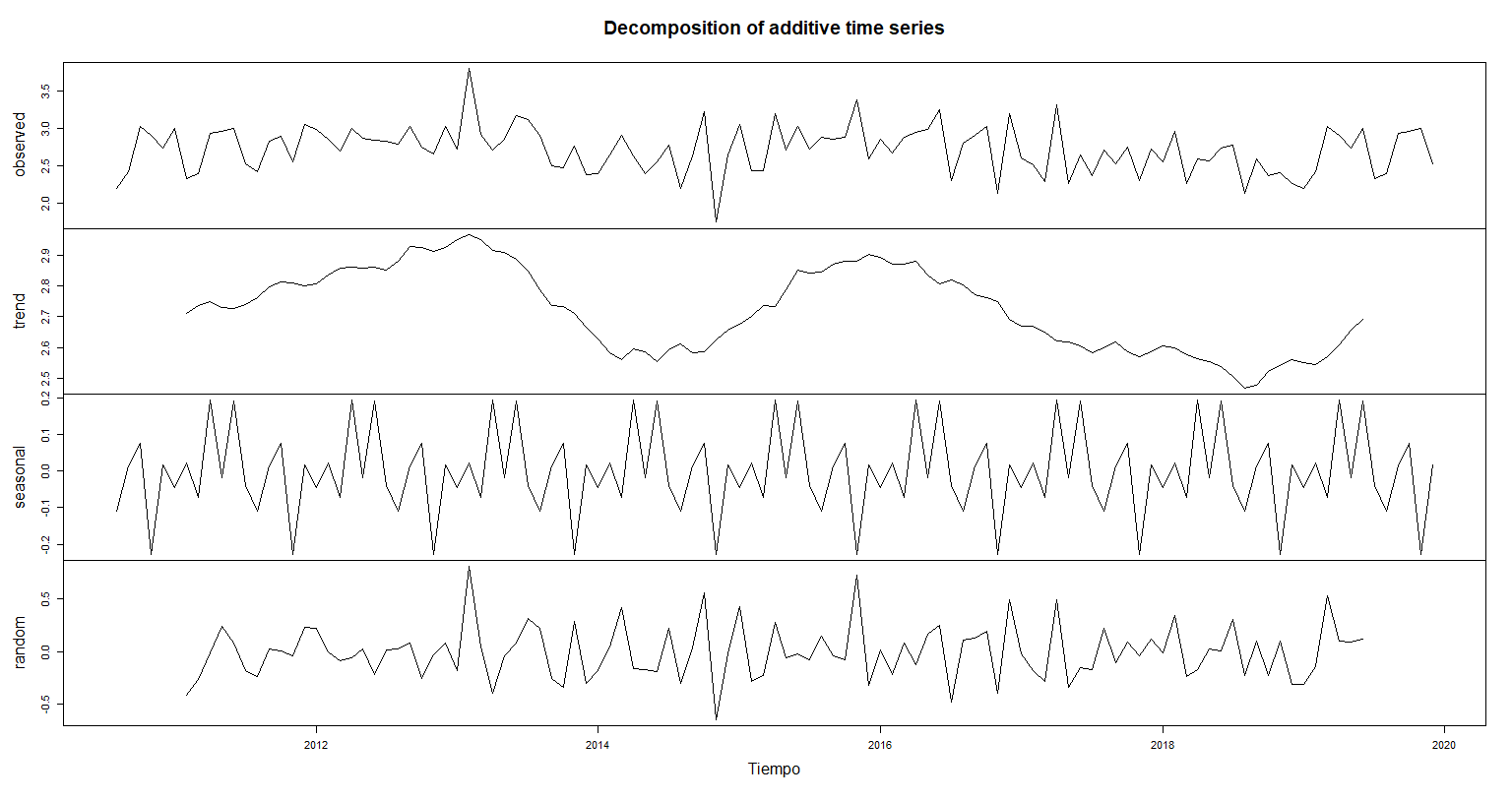
font.main =2) #modificaciones del titulogxm.decom.A <- decompose(golesxmes.ts)
plot(gxm.decom.A, xlab = "Tiempo",
sub = "Descomposición de los datos de goles por mes")Tendencia <- gxm.decom.A$trend
Estacionalidad <- gxm.decom.A$seasonal
Aleatorio <- gxm.decom.A$random
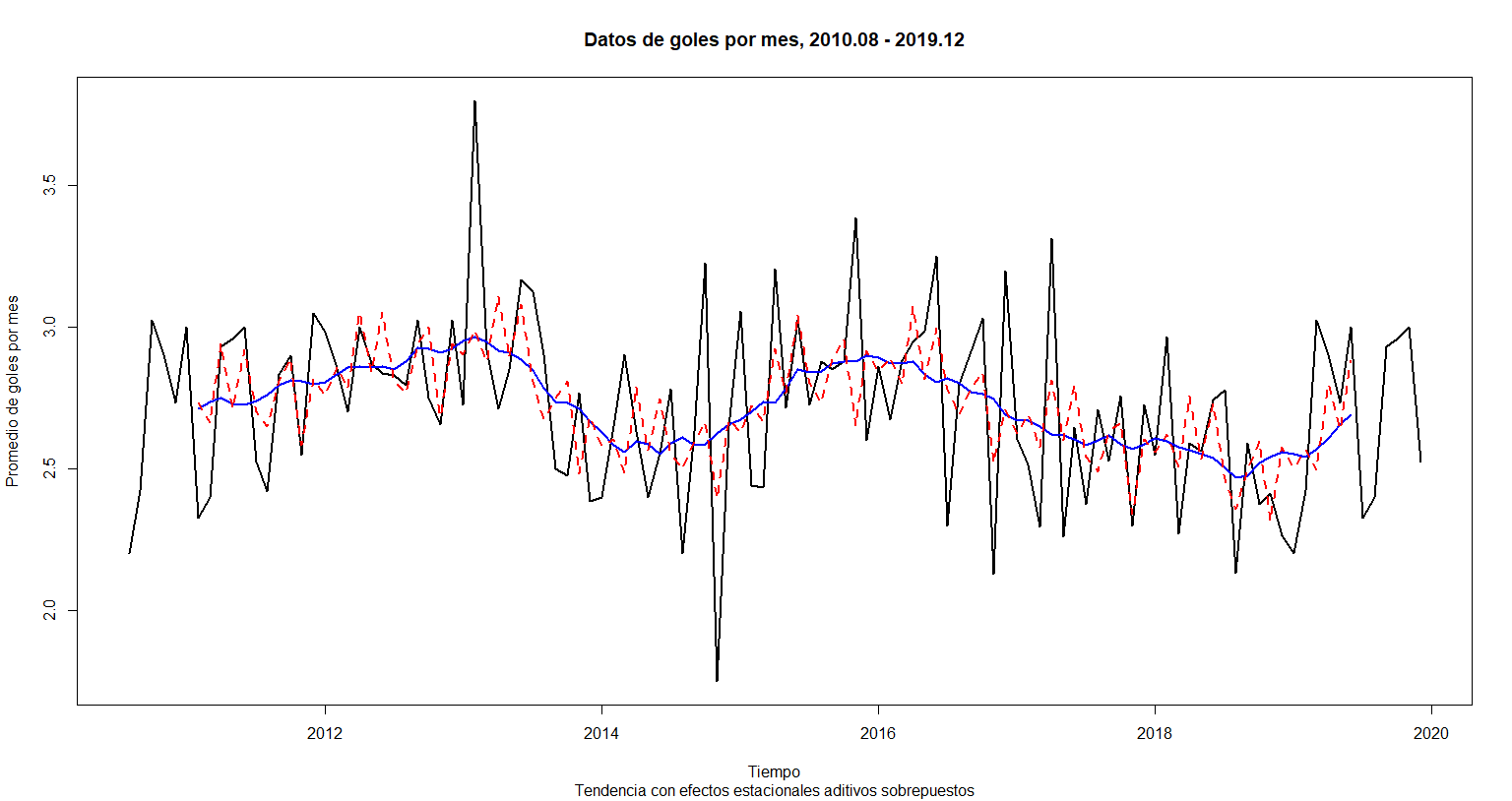
plot(golesxmes.ts,
xlab = "Tiempo", main = "Datos de goles por mes, 2010.08 - 2019.12",
ylab = "Promedio de goles por mes", lwd = 2,
sub = "Tendencia con efectos estacionales aditivos sobrepuestos") +
lines(Tendencia, lwd = 2, col = "blue") +
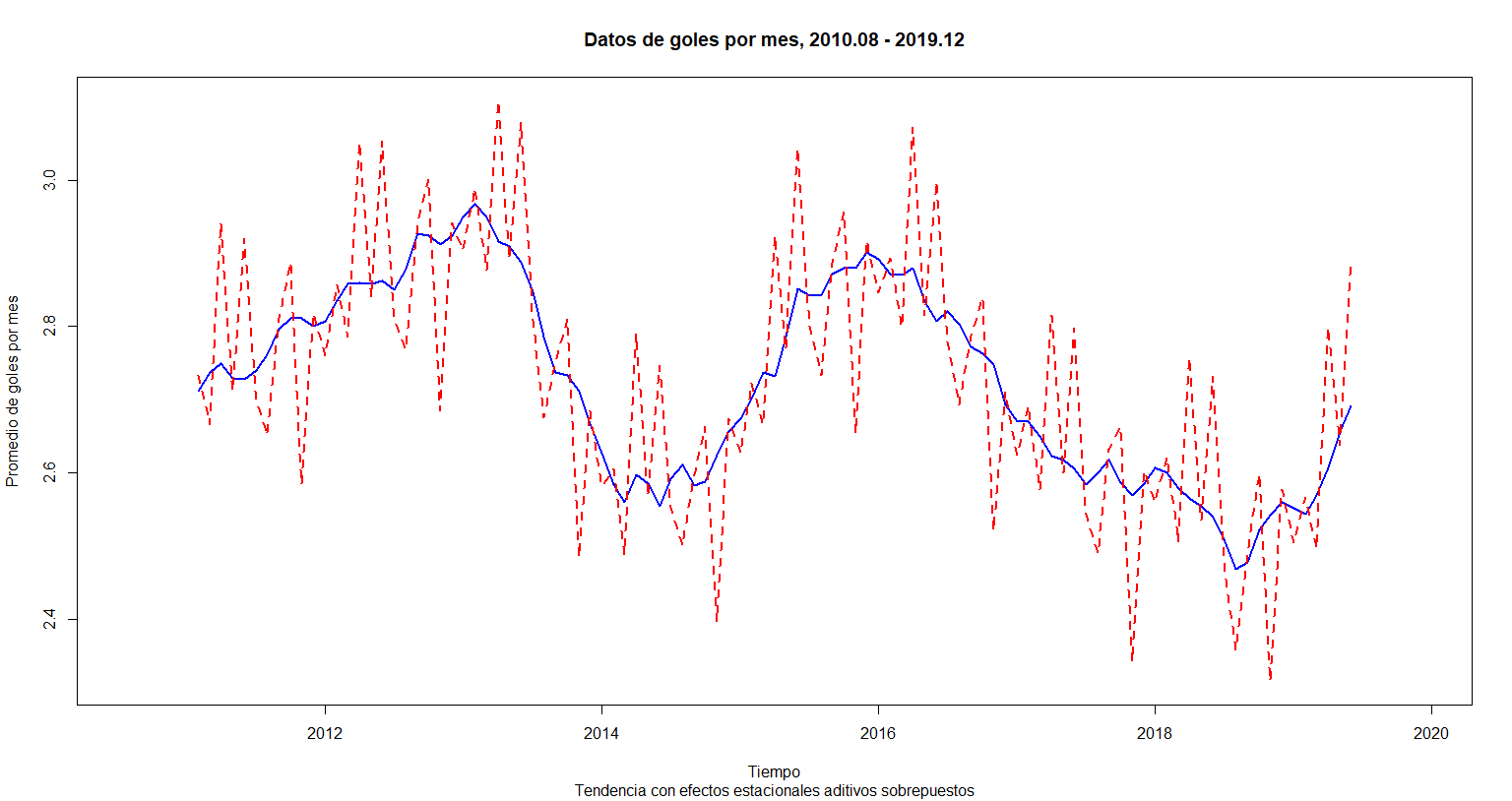
lines(Tendencia + Estacionalidad, lwd = 2, col = "red", lty = 2)ts.plot(cbind(Tendencia, Tendencia + Estacionalidad),
xlab = "Tiempo", main = "Datos de goles por mes, 2010.08 - 2019.12",
ylab = "Promedio de goles por mes", lty = 1:2,
col = c("blue", "red"), lwd = 2,
sub = "Tendencia con efectos estacionales aditivos sobrepuestos")Comprobamos un punto de la suma de las componentes con la serie de tiempo
(Tendencia[20] + Estacionalidad[20] + Aleatorio[20])## [1] 2.7
(golesxmes.ts[20])## [1] 2.7
plot(golesxmes.ts,
xlab = "Tiempo", main = "Datos de goles por mes, 2010.08 - 2019.12",
ylab = "Promedio de goles por mes", lwd = 2) +
lines(Tendencia, lwd = 2, col = "blue") +
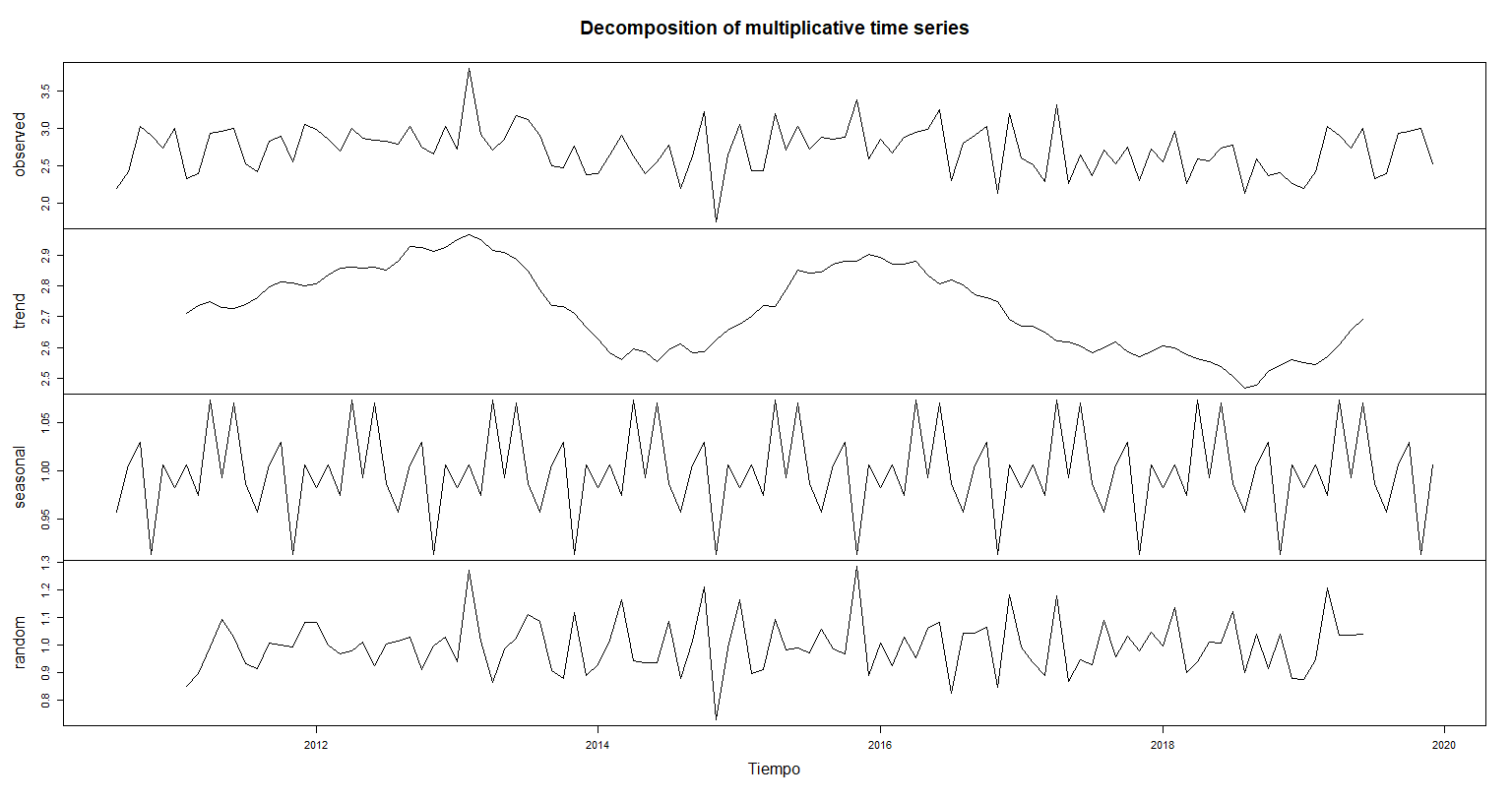
lines(Tendencia + Estacionalidad, lwd = 2, col = "red", lty = 2)gxm.decom.M <- decompose(golesxmes.ts, type = "mult")
plot(gxm.decom.M, xlab = "Tiempo",
sub = "Descomposición de los datos de goles por mes")Trend <- gxm.decom.M$trend
Seasonal <- gxm.decom.M$seasonal
Random <- gxm.decom.M$random
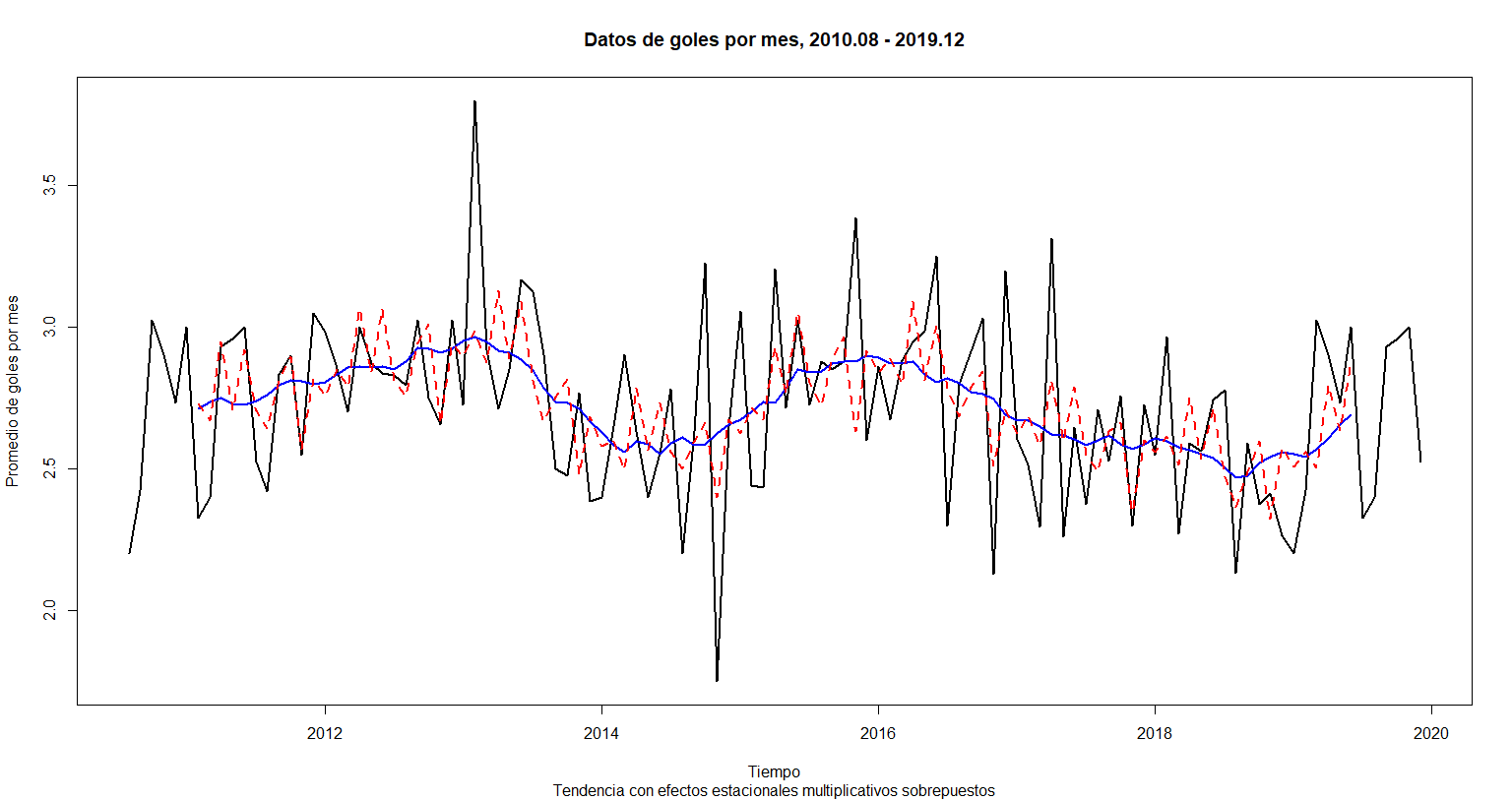
plot(golesxmes.ts,
xlab = "Tiempo", main = "Datos de goles por mes, 2010.08 - 2019.12",
ylab = "Promedio de goles por mes", lwd = 2,
sub = "Tendencia con efectos estacionales multiplicativos sobrepuestos") +
lines(Trend, lwd = 2, col = "blue") +
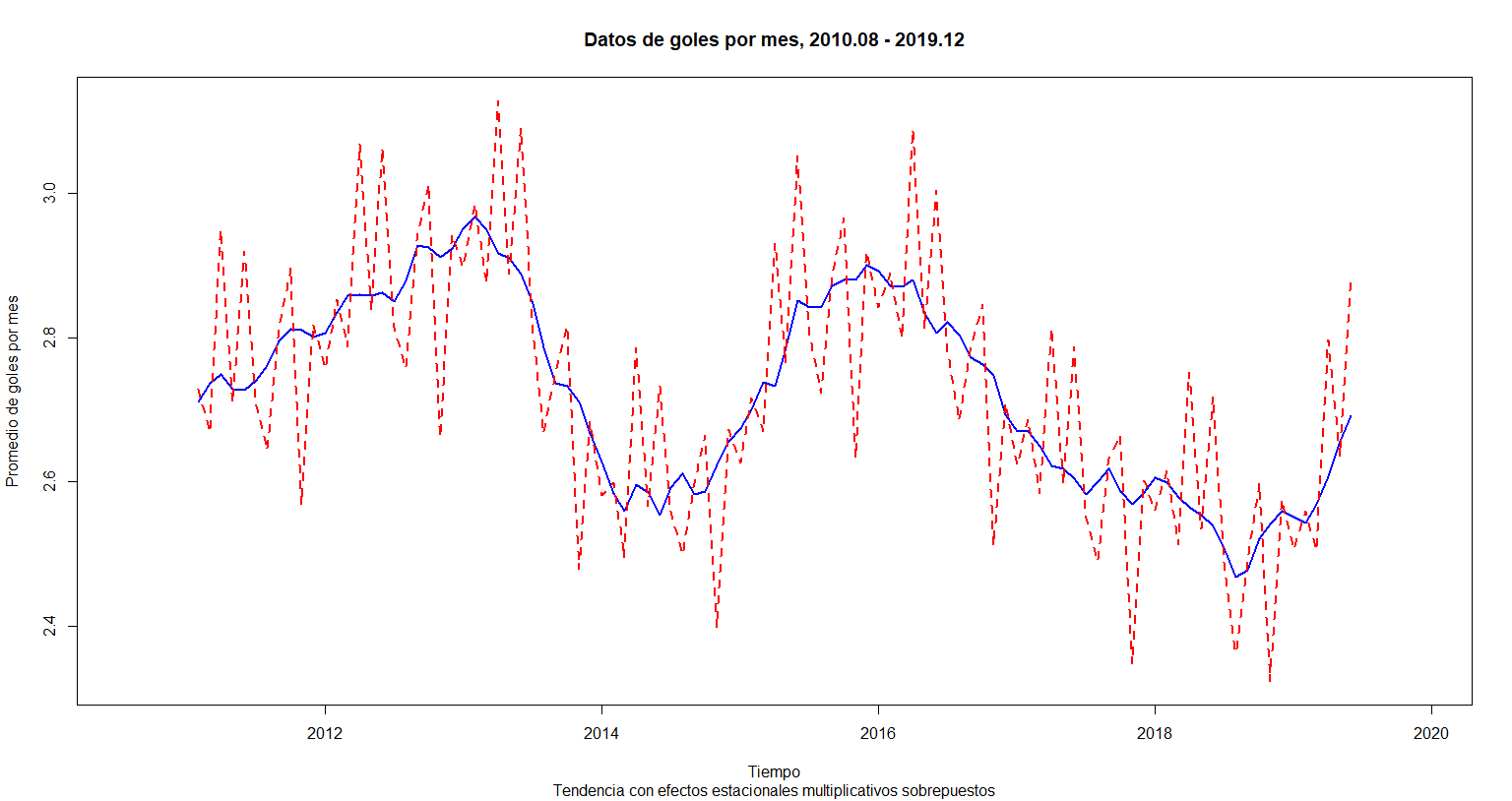
lines(Trend * Seasonal, lwd = 2, col = "red", lty = 2)ts.plot(cbind(Trend, Trend * Seasonal),
xlab = "Tiempo", main = "Datos de goles por mes, 2010.08 - 2019.12",
ylab = "Promedio de goles por mes", lty = 1:2,
col = c("blue", "red"), lwd = 2,
sub = "Tendencia con efectos estacionales multiplicativos sobrepuestos")Comprobamos un punto de la multiplicación de las componentes con la serie de tiempo
Trend[20] * Seasonal[20] * Random[20]## [1] 2.7
golesxmes.ts[20]## [1] 2.7
Ambos modelos arrojan el mismo resultado por lo que sería indistinto elegir entre uno u otro
Notemos que la frecuencia es 10 y no 12, ya que aunque la serie de tiempo se realiza tomando en cuenta los meses, las temporadas se juegan de agosto a mayo, por lo tanto como no se realizan juegos durante los meses de junio y julio sólo se toman en cuenta los 10 meses donde se generan los goles
library(mongolite)
library(dplyr)Importamos el csv
match.db <- read.csv("https://raw.githubusercontent.com/beduExpert/Programacion-R-Santander-2021/main/Sesion-07/Postwork/match.data.csv")Conectamos el cluster con la base de datos “match_games” y la colección “match”
connection <- mongo( collection = "match"
, db = "match_games"
, url = "mongodb+srv://equipo10:[email protected]/test")Verificamos que si no hay documentos agregue los datos del csv
if (connection$count() == 0) {
connection$insert(match.db)
}Consultamos el número de registros
connection$count()## [1] 3800
Armamos el cuerpo de la consulta con sintaxis de mongodb
query = c('{ "$or": [
{"home_team": "Real Madrid"}
, {"away_team": "Real Madrid"}
],
"date": "2015-12-20"
}')Realizamos la consulta y ‘find’ convierte el resultado de la colección a dataframe
q.response <- connection$find(query)Notamos que el Real Madrid solo jugó como local; contamos los goles y vemos quien fue el equipo contrincante
n.goles <-
q.response %>%
filter(home_team == "Real Madrid") %>%
pull(home_score) %>%
sum()
vs.team <-
q.response %>%
filter(home_team == "Real Madrid") %>%
pull(away_team)Vemos los resultados
cat(paste( "Cantidad de goles metidos el 20-12-2015 por el Real Madrid: "
, n.goles , "\n"
, "Contra el equipo: "
, vs.team
, sep = ""))## Cantidad de goles metidos el 20-12-2015 por el Real Madrid: 10
## Contra el equipo: Vallecano
if (n.goles > 4){cat(" ¡¡Fue una goleada!! ")}## ¡¡Fue una goleada!!
Desconectamos la conexión
connection$disconnect()Referencias:
https://cran.r-project.org/web/packages/mongolite/mongolite.pdf
https://jeroen.github.io/mongolite/query-data.html
https://jeroen.github.io/mongolite/manipulate-data.html
Link para la aplicacion Shiny: https://omar-magaa.shinyapps.io/Postwork8/
Debido a la identación y anidación que se genera al hacer el código se presenta por bloques comentado
library(shiny)
library(shinydashboard)
library(dashboardthemes)
library(shinythemes)
library(plotly)
customLogo <- shinyDashboardLogoDIY(
boldText = tags$a("Equipo 10",href="https://github.com/napoleonleal/R-BEDU-Project")
, mainText = ""
, textSize = 16
, badgeText = "BEDU"
, badgeTextColor = "white"
, badgeTextSize = 3
, badgeBackColor = "#000000"
, badgeBorderRadius = 5
)ui <- fluidPage(
# Creamos la pagina con un dashboard
dashboardPage( title = "Equipo 10",
# Definimos el header de la pagina
dashboardHeader(title = customLogo
),
# Creamos una SideBar y definimos los elementos que contendra
dashboardSidebar(
sidebarMenu(
menuItem( "Inicio"
, tabName = "home"
, icon = icon("home")),
menuItem( "Graficas de barras"
, tabName = "graficas"
, icon = icon("bar-chart")),
menuItem( "Goles casa - visitante"
, tabName = "post3"
, icon = icon("area-chart")),
menuItem( "Data Table"
, tabName = "data_table"
, icon = icon("table")),
menuItem( "Factores de Ganacias"
, tabName = "ganacias"
, icon = icon("money")),
menuItem( "Repositorios"
, tabName = "gh"
, icon = icon("github"))
)
), # Definimos el body del dashboar
dashboardBody(
shinyDashboardThemes(
# Especificamos el tema que vamos a utlizar para la aplicacion
theme = "purple_gradient"
),
# Definimos el cuerpo para cada tab del menu
tabItems(
# Inicio
tabItem(tabName = "home",
fluidRow(
column(8, align="center", offset = 2,
strong( h1("BIENVENIDO AL SHINY DEL EQUIPO 10"),
h2("AQUI PODRÁS INTERACTUAR CON NUESTROS RESULTADOS"),
tags$br(),
h2("INTEGRANTES DEL EQUIPO: "),
h3("María Magdalena Castro Sam"),
h3("Sergio Napoleón Leal"),
h3("Jesús Omar Magaña Medina"),
h3("Fernando Itzama Novales Campos"),
h3("Adrián Ramírez Cortés"),
h3("Efraín Soto Olmos")
),
img(src = "blob.png", height = 250, width = 250),
tags$style(type="text/css", "#string { height: 50px; width: 100%; text-align:center; font-size: 30px; display: block;}")
)
)
), # Grafica de barras de los goles
tabItem(tabName = "graficas",
fluidRow(
column(8, align="center",
offset = 2,
h1("Goles a favor y en contra por equipo")),
selectInput("x", "Selecciona el valor de x",
choices = c("Goles Locales",
"Goles Visitantes")),
plotlyOutput("grafica8",height = 800)
),
), # Graficas Postwork 3
tabItem(tabName = "post3",
fluidRow(
column(8, align="center", offset = 2,
strong( h1("Gráficas del PostWork 3"))),
box(title = "P(x) Marginal Equipo Local meta Gol",
plotlyOutput("plotPW1")),
box(title = "P(y) Marginal Equipo Visitante meta Gol",
plotlyOutput("plotPW2")),
box(title = "Figura 3.3 P(x∩y) conjunta",
plotlyOutput("plotPW3"))
)
), # Data table del archivo match.data.csv
tabItem(tabName = "data_table",
fluidRow(
column(8, align="center",
offset = 2,
titlePanel(h3("Data Table de la Liga Española"))),
dataTableOutput ("data_table")
)
), # Grafica de Momios
tabItem(tabName = "ganacias",
fluidRow(
column(8, align="center", offset = 2,
strong(
h1("Gráficas de los factores de ganancia mínimo y máximo"))),
column(9, align="right", offset = 2,
radioButtons("picture", "Tipo de momios:",
c("Escenario con momios máximos",
"Escenario con momios promedio"))
),imageOutput("imagenMomios")
)
), # Repositorios
tabItem(tabName = "gh",
fluidRow(
box(title= "Repositorio version GitHub",
tags$a(img(src= "git.png",
height = 320, width = 580),
href= "https://github.com/napoleonleal/R-BEDU-Project")),
box(title="Repositorio version HTML",
tags$a(img(src= "page.png", height = 320, width = 580),
href= "https://itzamango.github.io/postwork-equipo-10/"))
)
)
)
)
)
)server <- function(input, output) {
library(ggplot2)
library(dplyr)
library(viridis)
library(viridisLite)
# Leemos el archivo de los resultados de los partidos de la liga española desde 2010
# hasta 2020
df.resultado = read.csv("https://raw.githubusercontent.com/omar17md/ejemplo_1/main/df_resultado.csv") #Gráfico de goles
output$grafica8 <- renderPlotly({
if(input$x == "Goles Locales"){
p = ggplot(df.resultado, aes( x = home.score ) ) +
geom_bar(aes(fill = Result)) +
facet_wrap( ~ away.team ) +
labs(y = "Goles")+
scale_fill_discrete(name = "Resultados",
labels = c("Gano Visitante",
"Empate", "Gano Local"))
# +scale_y_continuous(limits = c(0,50))
}else{
p = ggplot(df.resultado, aes( x = away.score ) ) +
geom_bar(aes(fill = Result)) +
facet_wrap( ~ away.team ) +
labs(y = "Goles")+
scale_fill_discrete(name = "Resultados",
labels = c("Gano Visitante",
"Empate", "Gano Local"))
# +scale_y_continuous(limits = c(0,50))
}
ggplotly(p)
}) # Función para obtener la frecuencia y probabilidad
get.prob.df<- function(data, team, name.gol, name.prob){
team <- enquo(team)
data %>%
pull(!!team) %>%
table(., dnn = (name.gol)) %>%
as.data.frame %>%
mutate(!!name.prob := Freq/sum(Freq))
}
# Función para redondear 3 digitos
get.round <- function(data, digits){
data %>% mutate_if(is.numeric, round, digits=digits)
}
# Función para obtener la probabilidad conjunta en objeto tabla
get.prob.joint.tbl <- function(data, team.h, team.a, name.h, name.a){
data %>%
{table( team.h, team.a, dnn = c(name.h, name.a)) } %>%
prop.table
} # Gráficas del postwork3
# Leemos el archivo que se genero en el postwork2
data <- "https://raw.githubusercontent.com/napoleonleal/R-BEDU-Project/main/Postwork_2/Postwork_02.csv" %>%
read.csv %>%
mutate(Date = as.Date(Date, "%Y-%m-%d"))
# calculamos la probabilidad marginal de los goles metidos por locales:
prob.m.local <-
get.prob.df(data, FTHG, "Gol.Home", "P.Marginal")
prob.m.local %>% get.round(3)
# Creamos una función para gráficar los datos
plot.bar <- function(data, x.lab, y.lab, f.lab, title){
Goles <- data[1] %>% unlist()
Porcentaje <- (data[3]*100 ) %>% unlist %>% round(., digits=2)
Prob.Marginal <- data[3] %>% unlist() %>% round(., digits=4)
data %>%
ggplot() +
geom_bar(stat = 'identity') +
aes( x = Goles
, y = Porcentaje
, fill = Porcentaje
, text = paste("Prob Marginal", Prob.Marginal,
group = interaction(Goles, Porcentaje))
) +
labs( x = x.lab
, y = y.lab
, fill = f.lab
, title = title
) +
theme_minimal() +
theme( text = element_text(size=15)
,legend.title = element_text(size=10)
) +
scale_fill_viridis(name=f.lab, direction = 1)
} #Primera grafica del postwork3
output$plotPW1 <- renderPlotly({
plot.local = plot.bar(prob.m.local
, "Goles [n]"
, "Probabilidad de ocurrencia [%]"
, "%"
, "Probabilidad de anotación del equipo local" )
ggplotly(plot.local)
})
prob.m.visit <-
get.prob.df(data, FTAG, "Gol.Away", "P.Marginal")
prob.m.visit %>% get.round(3)
#Segunda grafica del postwork 3
output$plotPW2 <- renderPlotly({
plot.visit <- plot.bar(prob.m.visit
, "Goles [n]"
, "Probabilidad de ocurrencia [%]"
, "%"
, "Probabilidad de anotación del equipo visitante" )
ggplotly(plot.visit)
}) # Calculamos la probabilidad conjunta de que el equipo que juega en casa anote *'x'*
# goles y el equipo que juega como visitante anote '*y'* goles:
prob.joint <-
get.prob.joint.tbl(data, data$FTHG, data$FTAG, "Local", "Visitante")
prob.joint %<>% "*"(100) %>% round(2)
prob.joint %<>% as.data.frame() %>% rename(Probabilidad = Freq)
# Creamos la fucion para graficar el mapa de calor
plot.heat <- function(data, x.lab, y.lab, f.lab, title){
ggplot(data) +
aes( Local
, Visitante
, fill = Probabilidad
) + #gráficamos
geom_raster() +
labs( x = x.lab
, y = y.lab
, fill = f.lab
, title = title
) +
theme( text = element_text(size=18)
, legend.title = element_text(size=15)
) +
scale_fill_viridis( name=f.lab
, direction = 1 #, option = "H"
)
} # Tercera grafica del postwork 3
output$plotPW3 <- renderPlotly({
plot.mapa.calor <-
plot.heat( prob.joint
, "Local [goles]"
, "Visitante [goles]"
, "Probabilidad [%]"
, "Probabilidad Conjunta de anotación"
)
ggplotly(plot.mapa.calor) #versión interactiva
}) #Data Table
df = read.csv("https://raw.githubusercontent.com/napoleonleal/R-BEDU-Project/main/Postwork_8/match.data.csv")
output$data_table <- renderDataTable( {df},
options = list(aLengthMenu = c(5,25,50),
iDisplayLength = 50)
)
# Imagenes momios
output$imagenMomios <- renderImage({
if(input$picture == "Escenario con momios máximos"){
list(src = "www/momios1.png", height = 520, width = 1200)
}
else if(input$picture == "Escenario con momios promedio"){
list(src = "www/momios2.png", height = 520, width = 1200)
}
}, deleteFile = FALSE)
}
# Corremos la aplicacion
shinyApp(ui = ui, server = server)En la elaboración del proyecto fue evidente que en el área de análisis de datos es necesario no sólo conocimientos de programación sino también un entendimiento claro de conceptos matemáticos y estadísticos y sobre el área del negocio para poder dar una interpretación adecuada a los datos, puesto que de otra manera podría prestarse a conclusiones erróneas o que no aportan valor a los objetivos.
El análisis de las variables juega un papel importante, en nuestro caso el descubrir que las variables de los goles no son independientes dio pie a buscar un análisis más profundo, ya que en un partido hay muchos factores que intervienen tales como las tarjetas amarillas o rojas, una lesión que ponga a un jugador fuera de juego, partidos arreglados, corrupción, entre muchos otros.
Por esta razón asegurar la victoria solo basados en los goles metidos sería erróneo. Por lo tanto podemos concluir que los datos solo pueden dar una predicción segura con cierto margen de confianza hasta cierto punto y es necesario tomar en cuenta muchos elementos.
El análisis de datos en el sector del deporte es una industria creciente pues posee gran potencial. En el caso del presente trabajo, el saber que los modelos son acertados en cuanto a predecir las probabilidades de ganar o perder en algún partido posee gran importancia pues puede dar pie a generar estrategias para planificar el entrenamiento o poner énfasis en las jugadas frente a cierto equipo, o bien a generar apuesta con un porcentaje de riesgo relativamente bajo.
Identificar las variables dependientes es una parte importante, puesto que a partir de la relación entre ellas se encontrarán patrones y tendencias. Identificarlas para hacer una propuesta a partir de ello va a dar valor a los datos. De igual manera realizar series de tiempo y saber en qué situaciones aplicarlas es de gran importancia ya que puede dar un estimado sobre las variables estacionales que se pueden presentar en los datos y poder hacer predicciones significativas.
Otros datos importantes que pueden ayudar en el contexto del fútbol son los análisis físicos puesto que a través de estas estadísticas se pueden identificar puntos de mejora para los jugadores. La comunicación de estas estadísticas físicas permite tener un mejor entendimiento entre los miembros y al conocerse mejor se puede tener una mejor dinámica de equipo lo cual es de vital importancia en el futbol, así como ayudar a los jugadores a conocer áreas de potencial mejora y entrenamiento. Los análisis sobre las jugadas y pases durante los partidos pueden ayudar a tomar decisiones tácticas y a planear mejores entrenamientos para tener un mejor rendimiento en la cancha.
A pesar de que en el futbol existen muchas variables impredecibles que influyen en el resultado de un partido, el análisis de los datos puede ser de ayuda para obtener estadísticas importantes a tomar en cuenta para fijar cursos de acción futuros. El correcto análisis de los datos puede ayudar a que se puedan puedan tomar decisiones mas informadas y objetivas, tomando en cuenta el contexto de los jugadores y del pánorama deportivo actual.