-
Notifications
You must be signed in to change notification settings - Fork 54
Example: Harris Corner Detection
VisionCpp is a powerful tool to write Computer Vision algorithms for high performance computing. One really famous algorithm which has many applications is the Harris Corner detector [1]. Corners are important keypoints in a image. Those points can be used to detect objects, classify images, create panoramic scenes and generate 3D reconstruction.
The Harris Corner detector is based on the derivatives of the image. Below we show briefly what are the formulae to implement the Harris Corner detector:
![Harris Corner Detection formula] (https://raw.githubusercontent.com/wiki/codeplaysoftware/visioncpp/images/harris_formula.gif)
Where:
- Ix : Derivative in x direction. (Filter used for the derivative in the image below)
- Iy : Derivative in y direction. (Filter used for the derivative in the image below)
- w(x,y): summation mask between neighbour pixel
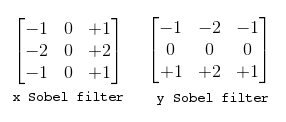
After computing the Matrix M, a score can be calculated for each window, to determine if it can possibly contain a corner using the formula below. Where det in the determinant of a matrix and trace is the sum of the diagonal elements.
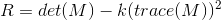
This algorithm is applied to each pixel, so it is possible to use the features of VisionCpp to implement it in parallel.
Let's go step by step how to implement the algorithm in VisionCpp (The full file which implements the Harris Corner Detector can be seen here).
- In all VisionCpp applications, first we need o decide our OpenCL-accelerator device which will execute our tree
// selecting CPU as OpenCL-accelerator device
auto dev = visioncpp::make_device<visioncpp::backend::sycl, visioncpp::device::cpu>();- Let's initialize our host data. We use OpenCV just to load and display the image. VisionCpp is designed to have fixed sizes, so we need to provide the size of the input image in advance.
// path to load the image using opencv
cv::Mat input = cv::imread(argv[1]);
// defining the image size constants
constexpr size_t COLS = 512;
constexpr size_t ROWS = 512;
// creating a pointer to store the results
std::shared_ptr<unsigned char> output(new unsigned char[COLS * ROWS],[](unsigned char* dataMem) { delete[] dataMem; });
// initialize an output image from OpenCV for displaying results
cv::Mat outputImage(ROWS, COLS, CV_8UC1, output.get());- Now we can define operations on the image. This is done by creating operation nodes which will then execute on the OpenCL accelerator. First we need to create our terminal nodes which will receive our host data.
// the node which gets the input data from OpenCV
auto in = visioncpp::terminal<pixel::U8C3, COLS, ROWS, memory_type::Buffer2D>(input.data);
// the node which gets the output data
auto out = visioncpp::terminal<pixel::U8C1, COLS, ROWS, memory_type::Buffer2D>(output.get());- We need now to convert our image to Greyscale. VisionCpp has already implemented operators to convert to Greyscale.
// convert to Float
auto frgb = visioncpp::point_operation<visioncpp::OP_U8C3ToF32C3>(in);
// convert to gray scale
auto fgray = visioncpp::point_operation<visioncpp::OP_RGBToGRAY>(frgb);- Now we can compute the derivatives x and y directions. The derivative is basically the difference between neighbour pixels, a really common way of computing the derivative of an image is to use the Sobel operators.
- Let's implement a 2D convolution which accepts any filter.
/// \brief this functor implements a convolution for a custom filter
struct Filter2D {
/// \param nbr - input image
/// \param fltr - custom filter
template <typename T1, typename T2>
float operator()(T1& nbr, T2& fltr) {
int hs_c = (fltr.cols / 2);
int hs_r = (fltr.rows / 2);
float out = 0;
for (int i2 = -hs_c, i = 0; i2 <= hs_c; i2++, i++)
for (int j2 = -hs_r, j = 0; j2 <= hs_r; j2++, j++)
out += (nbr.at(nbr.I_c + i2, nbr.I_r + j2) * fltr.at(i, j));
return out;
}
};- We can initialize our Sobel masks on the node and create the nodes which will store it on device.
// initializing the mask memories on host
float sobel_x[9] = {-1.0f, 0.0f, 1.0f, -2.0f, 0.0f, 2.0f, -1.0f, 0.0f, 1.0f};
float sobel_y[9] = {-1.0f, -2.0f, -1.0f, 0.0, 0.0f, 0.0f, 1.0f, 2.0f, 1.0f};
// initializing the node which store the masks on the device
auto px_filter = visioncpp::terminal<float, 3, 3, memory_type::Buffer2D, scope::Constant>(sobel_x);
auto py_filter = visioncpp::terminal<float, 3, 3, memory_type::Buffer2D, scope::Constant>(sobel_y);- Now we can apply our derivatives in x and y using our Filter2D functor.
// applying derivative in x direction
auto px = visioncpp::neighbour_operation<Filter2D>(fgray, px_filter);
// applying derivative in y direction
auto py = visioncpp::neighbour_operation<Filter2D>(fgray, py_filter);- Let's create the some simple operators (multiplication, power of 2, addition, subtraction) that will be used for our next tasks. Those operators are already implemented in VisionCpp, we are creating it again for tutorial purposes, showing that it is easy to create new operators.
// operator created to perform a power of 2 of the image
struct PowerOf2 {
template <typename T>
float operator()(T t) {
return t * t;
}
};
// operator for element-wise multiplication between two images
struct Mul {
template <typename T1, typename T2>
float operator()(T1 t1, T2 t2) {
return t1 * t2;
}
};
// operator to add two images
struct Add {
template <typename T1, typename T2>
float operator()(T1 t1, T2 t2) {
return t1 + t2;
}
};
// operator to subtract two images
struct Sub {
template <typename T1, typename T2>
float operator()(T1 t1, T2 t2) {
return t1 - t2;
}
};- Now we are able to compute the products of the derivatives.
- Ix² = Ix . Ix
- Iy² = Iy . Iy
- Ixy = Ix . Iy
auto px2 = visioncpp::point_operation<PowerOf2>(px);
auto py2 = visioncpp::point_operation<PowerOf2>(py);
auto pxy = visioncpp::point_operation<Mul>(px, py);- The next step is to compute the sums of the products of derivatives at each pixel. When VisionCpp uses neighbour_operation, it is recommended to break the tree before and after to increase the kernel occupancy.
// breaking the tree before convolution for a better use of shared memory
auto kpx2 = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(px2);
auto kpy2 = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(py2);
auto kpxy = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(pxy);
// Summing neighbours
float sum_mask[9] = {1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f};
auto sum_mask_node = visioncpp::terminal<float, 3, 3, memory_type::Buffer2D,scope::Constant>(sum_mask);
auto sumpx2 = visioncpp::neighbour_operation<Filter2D>(kpx2, sum_mask_node);
auto sumpy2 = visioncpp::neighbour_operation<Filter2D>(kpy2, sum_mask_node);
auto sumpxy = visioncpp::neighbour_operation<Filter2D>(kpxy, sum_mask_node);
// breaking the tree after convolution
auto ksumpx2 = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(sumpx2);
auto ksumpy2 = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(sumpy2);
auto ksumpxy = visioncpp::schedule<policy::Fuse, SM, SM, SM, SM>(sumpxy);- We have our matrix M computed:
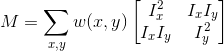
- And we can apply the formula: R = det(M) - k(trace(M))²
- det(M) is the determinant of the matrix which means: det(M) = Ix² . Iy² - Ixy . Ixy
- trace(M) is the sum of diagonal elements: trace(M) = Ix² + Iy²
- k is a tunable parameter, it is usually between 0.04 ... 0.06.
- The formula needs to be broken up into the appropriate VisionCPP operations.
// applying the formula det(M)-k*(trace(M)^2)
// det(M) = (ksumpx2*ksumpy2 - ksumpxy*ksumpxy)
auto mul1 = visioncpp::point_operation<Mul>(ksumpx2, ksumpy2);
auto mul2 = visioncpp::point_operation<PowerOf2>(ksumpxy);
auto det = visioncpp::point_operation<Sub>(mul1, mul2);
// trace(M) = ksumpx2 + ksumpy2
auto trace = visioncpp::point_operation<Add>(ksumpx2, ksumpy2);
// trace(M)^2
auto trace2 = visioncpp::point_operation<PowerOf2>(trace);
// k*(trace(M)^2)
auto k_node = visioncpp::terminal<float, memory_type::Const>(k_param);
auto ktrace2 = visioncpp::point_operation<Mul>(trace2, k_node);
// harris = det(M)-k*(trace(M)^2)
auto harris = visioncpp::point_operation<Sub>(det, ktrace2);- After the Harris is computed, we just need to threshold to get desirable corners.
// apply a threshold
// threshold parameter for the Harris
float threshold = 4.0f;
auto thresh_node = visioncpp::terminal<float, memory_type::Const>(static_cast<float>(threshold));
auto harrisTresh = visioncpp::point_operation<Thresh>(harris, thresh_node);
// convert to unsigned char for displaying purposes
auto display = visioncpp::point_operation<FloatToU8C1>(harrisTresh);- By assigning our display object to the terminal node of the graph, we tell the system to write the result of the graph to the display.
// assign to the output
auto k = visioncpp::assign(out, display);- After the tree is created we can finally execute our tree.
// execute expression tree
visioncpp::execute<policy::Fuse, 32, 32, 16, 16>(k, q);- We use OpenCV for visualizing the output of our graph.
// display result
cv::imshow("Harris", outputImage);- In the image [2] below it is possible to visualize the Harris corner detector applied to a chessboard.
| Reference Image | Harris Corner Detector |
|---|---|
 |
 |
VisionCpp is a computer vision framework which allows the user to create their own operators for developing high-level applications. Like many computer vision algorithms, the Harris Corner detector can be implemented as an operation that can be applied to each pixel in parallel. The tree-based model enables fusion of kernels by the compiler to produce highly-optimized kernels to be executed on OpenCL-accelerated platforms, enabling the creation of high-performance applications for computer vision.
[1] Harris, C., and M. Stephens. "A Combined Corner and Edge Detector." PDF. Proceedings of the 4th Alvey Vision Conference. pp. 147–151.
[2] https://commons.wikimedia.org/wiki/File:ExperimentalChessbaseChessBoard.png