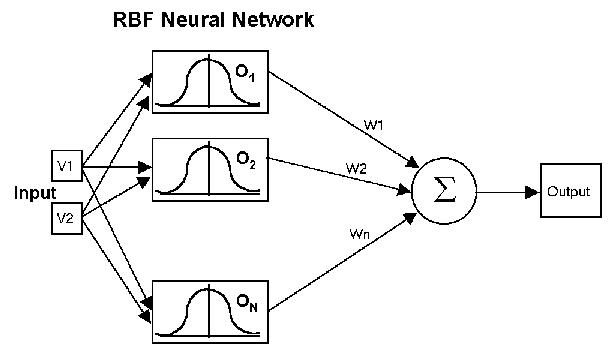
RBF_networks

RBF networks have inpug neurons, one hidden layer where each node is an RBF (Radial Basis Function) and one output neuron. We use Gaussians to model the receptive fields for neurons, so that nodes will fire strongly if the input is close to them, less strongly if the input is further away and not at all if it is even further away. The main idea is to map a input space in a higher dimension output space, but this higher dimension should be less than the number of training samples (if not overspecialization).

The output neuron acts like a normal perceptron. Therefore, the training of the network can be divided in two stages:

1. Training of RBF positions (mu of each RBF node). Unsupervised learning where we will use Competitive Learning.
2. Training of the perceptron (linear combination). Supervised learning where Least Squares method will be use for batch learning, and the delta rule for online learning.

In RBF_functions.py the RBF NN was implemented from scratch. We had the possibility to use batch learning, online learning, competitive learning, or fix the positions of the RBF nodes.

In order to study the performance of the NN we can run RBF_NN_implementation.py. In this script we approximate the functions sin(2x) and square(2x) using RBF NN.

Requirements

• numpy
• matplotlib

Run code

In order to run RBF_NN_implementation.py we have to specify the parameters of the algorithm in the arguments:

--n_nodes N_NODES

--learning_rate LEARNING_RATE

--sin_or_square SIN_OR_SQUARE

--sigma_RBF_nodes SIGMA_RBF_NODES

--batch_or_online_learning BATCH_OR_ONLINE_LEARNING

--n_epochs_online_learning N_EPOCHS_ONLINE_LEARNING

--use_CL USE_CL

--n_epochs_CL N_EPOCHS_CL

--plot_train_results PLOT_TRAIN_RESULTS

--plot_test_results PLOT_TEST_RESULTS

--verbose VERBOSE

--add_noise ADD_NOISE

Example:

python RBF_NN_implementation.py --n_nodes 11 --learning_rate=0.01 --sin_or_square sin --sigma_RBF_nodes 1 --batch_or_online_learning batch --use_CL False

Output:

Conclusions

• Batch learning will always make more accurate predictions than online learning.
• Delta learning performs better with more number of epochs.