-
Notifications
You must be signed in to change notification settings - Fork 9
Why is the default smoothing method "REML" rather than "GCV.Cp"?
As of version 2.2.14 dsm switched from using method="GCV.Cp" to method="REML" for smoothness selection. This change was after some serious experimentation by me (Dave Miller), discussion with the author of mgcv (Simon Wood) and review of available literature. The aim of this document is to outline why this change was made and why it was a good idea.
The discussion below is relatively technical and readers may want to consult Simon Wood's excellent "Generalized Additive Models: An Introduction with R" while reading.
dsm uses mgcv to do all its model fitting. mgcv has a number of options for selecting the smoothness of terms in the model. Smoothness selection method is specified via the method= argument and has the following options: "GCV.Cp", "GACV.Cp", "REML", "P-REML", "ML" and "P-ML". These methods can be separated into two groups: "prediction error" ("GCV.Cp" and "GACV.Cp") and "likelihood" ("REML", "P-REML", "ML" and "P-ML"). Here we'll just address "GCV.Cp" vs. "REML" (though similar arguments can be levelled in favour of "ML" vs "GCV.Cp". mgcv uses "GCV.Cp" as a default, though this is mainly for backwards compatibility (Simon Wood, pers. comm.).
Both REML and GCV try to do the same thing: make the smooths in your model just wiggly enough and no wigglier. It has been shown that GCV will select optimal smoothing parameters (in the sense of low prediction error) when the sample size is infinite. In practice there is presumably some sample size at which this asymptotic result kicks in, but few of us have data of that size. At smaller (finite) sample sizes GCV can develop multiple minima making optimisation difficult and therefore tends to give more variable estimates of the smoothing parameter. GCV also tends to undersmooth (i.e., smooths are more wiggly than they should be), as it penalizes overfit weakly (which makes sense for a prediction error based critera, where you want your model to fit your data well). This was shown in work by Phil Reiss and Todd Ogden (2009) as well as Simon Wood (2011). They also showed that REML (and ML, marginal likelihood) penalize overfitting more and therefore have more prounounced optima, leading to fewer optimisation issues and less variable estimates of the smoothing parameter.
This is best illustrated in this figure from Wood (2011) which shows the (log) smoothing parameter vs. REML and GCV. The ticks on the horizontal axis show where the optimum smoothing parameter lies for each example data set (profile of the REML/GCV criteria shown as lines). The REML ticks are close together and the lines all look similar. For GCV this is not the case.
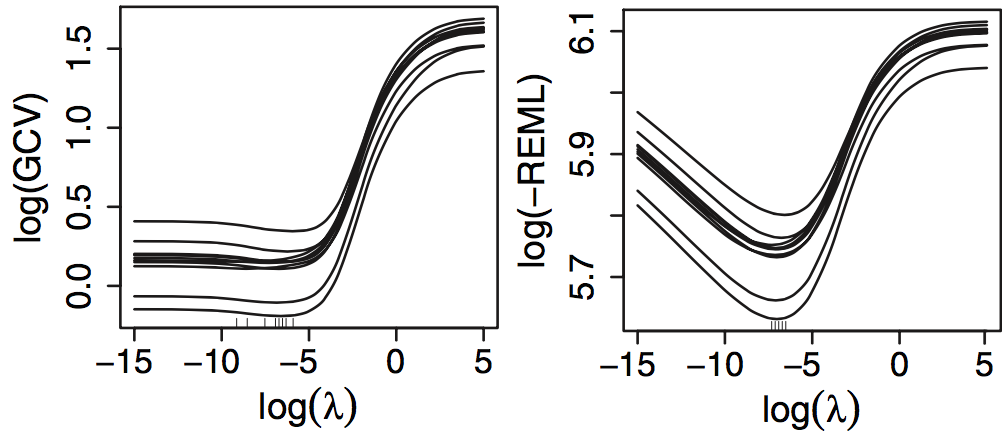
Section 1.1 of Wood (2011) gives an overview of these issues, though the rest of the paper is somewhat technical.
In practice I've analysed multiple datasets using both REML and GCV and in some cases have seen very different results when it comes to model and term selection. If GCV is prone to undersmoothing at finite sample sizes, then we will end up fitting models that are more wiggly than we want. Overfitting is surely something we want to avoid. It is not clear how many datasets (or what particular type of data) is vulnerable to this issue, but we (Distance Development Team) thought it best to switch to REML by default to avoid potential overfitting and highly variable smoothing parameter estimates.
Note that moving to REML, we need to be careful about model comparison. Models fitted with REML cannot be compared by their REML scores when their unpenalized components are different. In practice this means that models that use a shrinkage basis (e.g., "ts" or "cs") for all terms in the model or that use select=TRUE are fine but other models are not.
If marginal likelihood (ML) is used, we can compare those scores.
One can compare AIC (extracted using the AIC() function in R) of models fitted with REML or ML (or GCV), though obviously this is not the only model selection step!
- Reiss, P.T. and Ogden, R.T. (2009) Smoothing parameter selection for a class of semiparametric linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71, 505–523. pdf
- Wood, S.N. (2006) Generalized Additive Models. CRC Press.
- Wood, S.N. (2011) Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73, 3–36. pdf