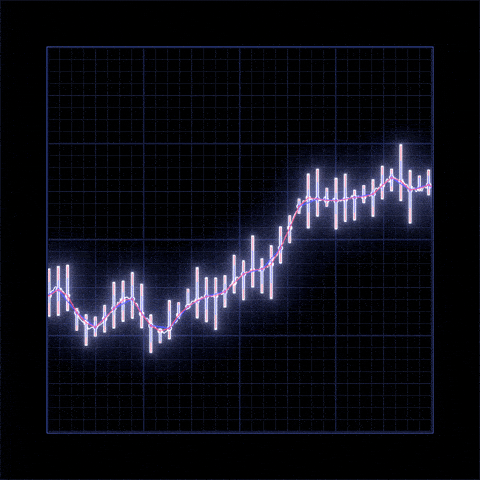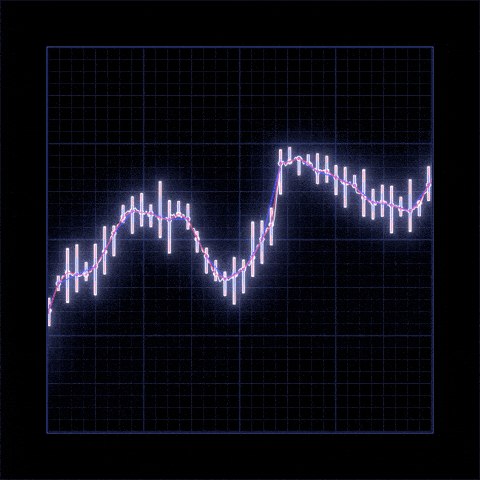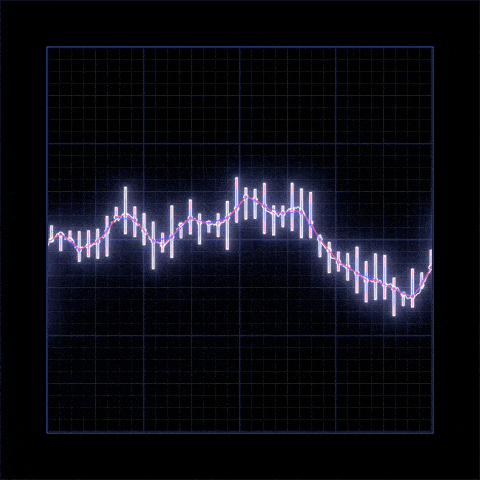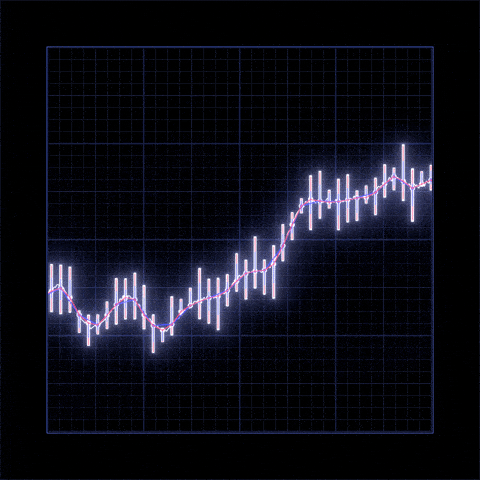AlmaBetter Verfied Project - Yes bank closing price prediction
Yes Bank is a well-known bank in the Indian financial domain. Since 2018, it has been in the news because of the fraud case involving Rana Kapoor. Owing to this fact, it was interesting to see how that impacted the stock prices of the company and whether Time series models or any other predictive models can do justice to such situations. This dataset has monthly stock prices of the bank since its inception and includes closing, starting, highest, and lowest stock prices of every month. The main objective is to predict the stock’s closing price of the month.
Dataset : Yes BankThis Project include one colab file where all the python coding is present.
Performed exploratory data analysis using varius visualization plots.
Trained machine learning model using Linear regression with regulerization (Ridge, Lasso and Elastic-net).
EDA stands for Exploratory Data Analysis. It is a crucial step in the data analysis process where the primary objective is to gain a better understanding of the data before applying any statistical modeling or hypothesis testing. EDA involves examining and visualizing the data through various techniques to uncover patterns, identify outliers, detect missing values, assess data quality, and understand the relationships between variables. By conducting EDA, data analysts can make informed decisions about data preprocessing, feature engineering, and modeling strategies, ultimately leading to more accurate and meaningful insights. EDA plays a fundamental role in data-driven decision-making and helps guide subsequent steps in the data analysis pipeline.
Linear regression is a statistical modeling technique used to understand the relationship between a dependent variable and one or more independent variables. It assumes a linear relationship between the variables, where the goal is to find the best-fitting line that minimizes the differences between the observed data points and the predicted values. By estimating the coefficients and intercept of the line, linear regression allows for the prediction of the dependent variable based on the values of the independent variables. It also provides insights into the strength and direction of the relationships, significance of variables, and the overall model performance. Linear regression is widely used in various fields for prediction, forecasting, and understanding the impact of variables on the outcome of interest.
Regularization techniques such as Ridge, Lasso, and ElasticNet are commonly used in machine learning and regression analysis to address the problem of overfitting and improve model performance.
Ridge Regression, also known as L2 regularization, adds a penalty term to the loss function that is proportional to the square of the magnitude of the coefficient values. This penalty term helps to reduce the magnitude of the coefficients, effectively shrinking them towards zero. Ridge regression can help alleviate multicollinearity issues and provide more stable estimates.
Lasso Regression, also known as L1 regularization, adds a penalty term to the loss function that is proportional to the absolute value of the coefficient values. Unlike Ridge, Lasso can perform feature selection by driving some of the coefficient values to exactly zero. This makes Lasso useful for models that have many irrelevant features or when interpretability is important.
ElasticNet combines the Ridge and Lasso regularization techniques by adding a penalty term that is a linear combination of the L1 and L2 penalty terms. It provides a balance between Ridge and Lasso, allowing for both coefficient shrinkage and feature selection. The ElasticNet penalty is controlled by a parameter called the mixing parameter, which determines the weight of the L1 and L2 penalties.
A decision tree is a machine learning algorithm used for both classification and regression tasks. It represents a flowchart-like structure, where each internal node represents a feature or attribute, each branch represents a decision rule, and each leaf node represents an outcome or a class label. The decision tree recursively partitions the data based on the values of different features, with the goal of maximizing the separation between different classes or minimizing the prediction error. By following the decision path from the root node to a leaf node, the decision tree can make predictions or assign class labels to new instances based on the learned rules. Decision trees are intuitive, interpretable, and capable of handling both categorical and numerical features, making them widely used in various domains for their simplicity and ability to capture complex decision-making processes.
Random Forest is a powerful machine learning algorithm that combines multiple decision trees to make predictions. It works by constructing an ensemble of decision trees, each trained on a random subset of the data and using a random subset of features. Random Forest leverages the principle of "wisdom of the crowd" by aggregating the predictions from individual trees to produce a final prediction. This approach helps to reduce overfitting and increase the model's generalization ability. Random Forest is suitable for both classification and regression tasks, providing accurate and robust predictions even in the presence of noisy or high-dimensional data. It also allows for feature importance assessment, enabling insights into which features contribute the most to the prediction. Random Forest is widely used in various domains due to its flexibility, scalability, and ability to handle complex relationships within the data.
In linear regression, several metrics are commonly used to evaluate the model's performance and assess the goodness of fit. Here's a brief explanation of some of the key metrics:
Mean Squared Error (MSE): MSE measures the average squared difference between the predicted and actual values. It provides a measure of the overall model accuracy, with lower values indicating better performance. However, MSE is sensitive to outliers since it squares the errors.
Root Mean Squared Error (RMSE): RMSE is the square root of the MSE, which gives the average magnitude of the prediction errors in the original units of the dependent variable. RMSE is easier to interpret since it is on the same scale as the dependent variable.
Mean Absolute Error (MAE): MAE computes the average absolute difference between the predicted and actual values. It is less sensitive to outliers compared to MSE since it doesn't square the errors. Like RMSE, MAE is also on the same scale as the dependent variable.
R-squared (R2): R-squared represents the proportion of the variance in the dependent variable that is explained by the independent variables in the model. It ranges from 0 to 1, with higher values indicating a better fit. However, R-squared can be misleading when the model is overfitting or when comparing models with different numbers of predictors.
Adjusted R-squared (Adjusted R2): Adjusted R-squared adjusts the R-squared value by considering the number of predictors and the sample size. It penalizes the addition of unnecessary predictors, making it a more reliable measure when comparing models with different numbers of predictors. Adjusted R-squared values closer to 1 indicate a better balance between model fit and complexity.
High Level Document(HLD) for Yes bank closing price prediction : Word Document .
Our main motive of the project was to predict the stock's closing price of the month. To determine the YES bank's stock’s future value on the national stock exchange. The advantage of a successful prediction of a stock's future price could results insignificant profit. The efficient-market hypothesis recommends that stock costs mirror all right now accessible data and any value changes that are not founded on recently uncovered data subsequently are an unpredictable. We have to build model which help us to predict the future stock prices.
The stock market is known for being volatile, dynamic, and nonlinear. Accurate stock price prediction is extremely challenging because of multiple (macro and micro) factors, such as politics, global economic conditions, unexpected events, a company’s financial performance, and so on. But, all of this also means that there’s a lot of data to find patterns in. So, financial analysts, researchers, and data scientists keep exploring analytics techniques to detect stock market trends. This gave rise to the concept of algorithmic trading which uses automated, pre-programmed trading strategies to execute orders.
The Challenge we face is due to small dataset so it’s difficult to get good model accuracy In EDA part we observed that :
- There is increase in trend of Yes Bank's stock's Open price till 2018 and then sudden decrease.
- We observed that open vs close price graph concluded that after 2018 yes bank's stock hitted drastically.
- Linear regressor with highest accuracy - 99.2%
Ridge regression accuracy - 99.23%
ElasticNet accuracy - 96.89%
Decision tree regressor accuracy - 97.64%
Random Forest accuracy - 98.50
Gradient Boost accuracy - 98.33
Xtream Gradient Boost accuracy - 98.45
Overall, we can say that Linear Regressor is the best model among all regression model which gives around 99.28% accuracy of predicting stock price of our dataset.