-
Notifications
You must be signed in to change notification settings - Fork 137
Reconstruction
All the functionalities described in this tutorial can be used interactively
in the geobox software bundled in Geogram.

The raw output of a 3D scanner is a pointset, that can be noisy, that
can have alignment errors, and that can have spurious points. The
image shows the raw input used to reconstruct the famous "Armadillo"
mesh. One can find it
here (as well as many
others, including the "Bunny" and the "Dragon"), pick the "range
data". It has in the same directory a ".conf" file with metadata. The
"geobox" utility bundled with Geogram can directly load a ".conf"
files, and transform and merge all the pointsets referred by it. As
can be seen, this file contains a lot of outliers. One can get rid of
them by invoking the filter_outliers command of "geobox". This
command finds the N nearest neighbors of each point, and discards
the points for which the N-th neighbor is further away than a
certain threshold distance R. It is implemented as follows:
void filter_outliers(Mesh& M, index_t N=70, double R=0.01) {
mesh_repair(M, GEO::MESH_REPAIR_COLOCATE, 0.0);
NearestNeighborSearch_var NN = new BalancedKdTree(3); // 3 is for 3D
NN->set_points(M.vertices.nb(), M.vertices.point_ptr(0));
vector<index_t> remove_point(M.vertices.nb(), 0);
double R2 = R*R;
parallel_for_slice(
0,M.vertices.nb(),
[&M,N,&NN,R2,&remove_point](index_t from, index_t to) {
vector<index_t> neigh(N);
vector<double> neigh_sq_dist(N);
for(index_t v=from; v<to; ++v) {
NN->get_nearest_neighbors(
N, M.vertices.point_ptr(v),
neigh.data(), neigh_sq_dist.data()
);
remove_point[v] = (neigh_sq_dist[N-1] > R2);
}
}
);
M.vertices.delete_elements(remove_point);
}First step eliminates duplicated vertices. Then, a KD-tree is constructed,
and queried in parallel. We use the sliced version of Geogram's
parallel_for, so that the neigh and neigh_sq_dist vectors can be
reused within the same slice (this reduces memory allocation / deallocation).
It fills the remove_point vector that indicates which point should be
discarded.

Pointsets obtained from 3D scanning are often composed of multiple scans, that need to be registered. Data can exhibit small registering errors, that create zones with mutliple overlapping layers of points that are slightly shifted (the surface has a certain "thickness" in these zones). Geogram includes a "point set smoothing" function that projects each point onto the least-square fitted plane of its neighbors. The function, declared in geogram/points/co3ne.h, works as follows:
#include <geogram/points/co3ne.h>
...
Co3Ne_smooth(mesh, nb_neighbors, nb_iterations);The function is part of Co3Ne (Concurrent Co-Cones) algorithm, used for both estimating normals, smoothing the pointset and reconstructing the surface (more on this in next paragraph).
Geogram includes two different algorithms for surface reconstruction:
-
Co3Ne [1] (Concurrent Co-Cones), that computes a restricted Voronoi diagram in parallel, without computing any 3D Delaunay triangulatoin, by exploiting the "radius of security" theorem that requires nothing else than a KD-tree [2];
-
Poisson surface reconstruction [3],[4], that solves a Poisson equation with Neumann boundary conditions on an adaptive grid. Poisson reconstruction needs oriented normals, one can use the first phase of Co3Ne to estimate them.
The Co3Ne reconstruction function is implemented in geogram/points/co3ne.h. Typically it is called as follows:
Co3Ne_smooth(mesh, nb_neighbors, nb_iterations);
Co3Ne_reconstruct(mesh, radius);Since Co3Ne is sensitive to alignment errors, first we smooth the pointset (typically with
30 neighbors and 2 iterations). The radius parameter corresponds to the maximum length of
a reconstructed edge.
Poisson reconstruction is implemented in the bundled code from Misha Kazhdan, with a wrapper
class PoissonReconstruction declared in geogram/third_party/PoissonRecon/poisson_geogram.h:
Mesh points;
points.copy(mesh,false,MESH_VERTICES);
Co3Ne_compute_normals(points, 30, true);
mesh.clear();
PoissonReconstruction poisson;
poisson.set_depth(depth);
poisson.reconstruct(&points, &mesh);Poisson reconstruction needs oriented normals. To compute them, we use Co3Ne.
The depth parameter corresponds to the number of levels in the octree used by Poisson reconstruction
(typically 8).


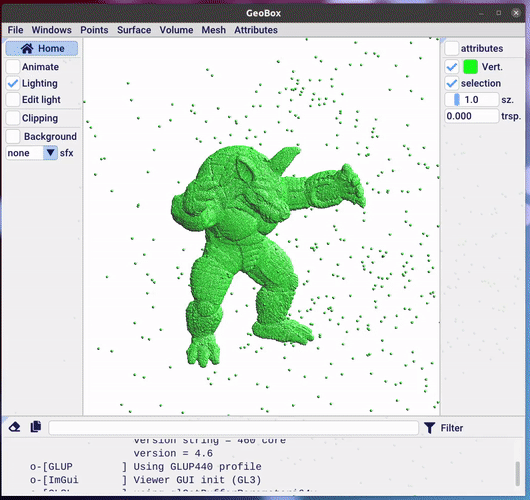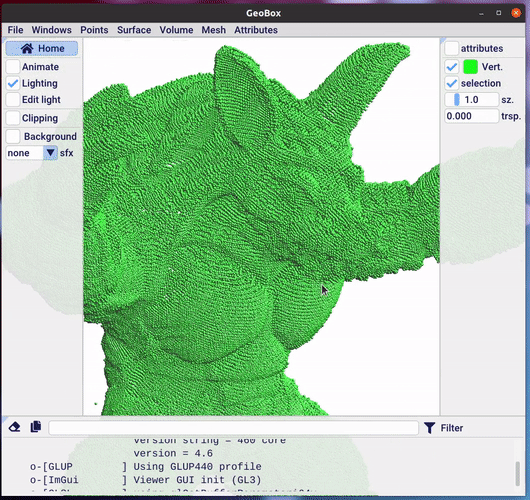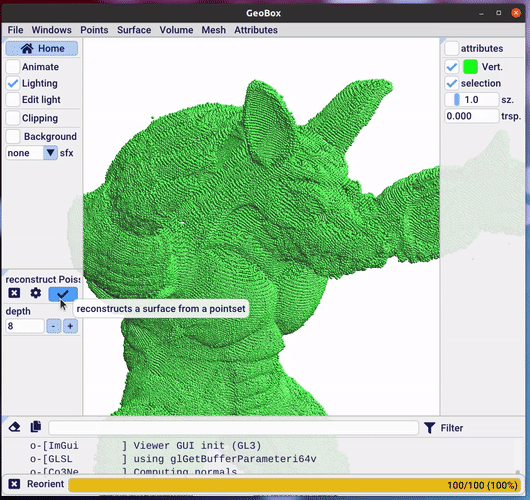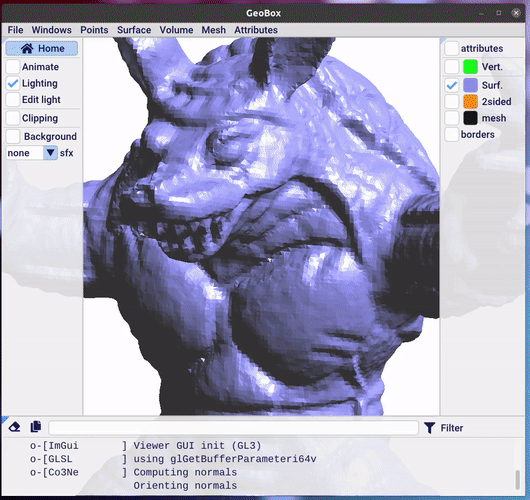
It all depends on the data, this is the reason why we keep both methods in Geogram. For the Armadillo pointset (top image), there are some registration errors and remaining outliers. Poisson reconstruction does a good job for smoothing the problematic points without losing geometric details, whereas Co3Ne reconstruction, that has no choice than using the existing points, exhibits some artifacts. For the Horse pointset (bottom image), the pointset is clean, but has a huge variation of density. This causes bulges in Poisson reconstruction, whereas Co3Ne reconstruction nicely interpolates the pointset.
[1] Surface reconstruction by computing restricted Voronoi cells in parallel, Dobrina Boltcheva &nd Bruno Lévy, Computer Aided Design, 2017, HAL
[2] Variational Anisotropic Surface Meshing with Voronoi Parallel Linear Enumeration, Bruno Lévy, Nicolas Bonneel, IMR, 2012, HAL
[3] Poisson surface reconstruction, Michael Kazhdan, Matthew Bolitho and Hugues Hoppe, Computer Graphics Forum, 2006
[4] An Adaptive Multi-Grid Solver for Applications in Computer Graphics, Michael Kazhdan and Hugues Hoppe, Computer Graphics Forum, 2018, code