-
Notifications
You must be signed in to change notification settings - Fork 136
Mesh

Geogram as a general-purpose mesh data structure, that can represent
surfacic and volumetric meshes, with triangles or polygonal facets for
the surfacic part, and with tetrahedra, hexahedra, prisms and pyramids
for the volumetric part. It is implemented in the class Mesh, declared
in geogram/mesh/mesh.h.
Functions to load and save meshes are declared in geogram/mesh/mesh_io.h:
bool mesh_load(
const std::string& filename, Mesh& M,
const MeshIOFlags& ioflags = MeshIOFlags
);
bool mesh_save(
const Mesh& M, const std::string& filename,
const MeshIOFlags& ioflags = MeshIOFlags()
);where MeshIOFlags is a class used to specify which mesh elements
(vertices, edges, facets, volumetric cells) and which attributes to
load/save.
Geogram supports the following mesh file formats:
| extension | comment |
|---|---|
| .obj | Alias Wavefront file format |
| .mesh | LM5/LM6 Gamma mesh file format (ascii) |
| .meshb | LM5/LM6 Gamma mesh file format (binary) |
| .ply | ASCII and binary, simple and double precision |
| .off | geomview OFF file format |
| .stl | ASCII and binary |
| .xyz | ASCII point cloud |
| .pts | Like .xyz, but each line starts with "v " |
| .tet | ASCII file format for hybrid volumetric meshes |
| .geogram | Native file format, can save attributes |
It is possible to add your own formats by subclassing the MeshIOHandler
class, and using the geo_register_MeshIOHandler_creator() macro. One
can refer to the function mesh_io_initialize() at the end of
geogram/mesh/mesh_io.cpp for an example.
In Geogram, meshes are implemented using incidence and adjacency arrays.
- the incidence array stores the facet-to-vertex relations. It can be queried by the function
M.facets.vertex(f,lv)wherefis a facet index andlva local vertex index in the facet. - the adjacency array stores the facet-to-facet relations. It can be queried by the function
M.facets.adjacent(f,le)wherefis a facet index andlea local edge index in the facet.
For instance, one can iterate on all the vertices of all facets of a triangulated mesh as follows:
for(index_t f=0; f<M.facets.nb(); ++f) {
for(index_t lv=0; lv<3; ++lv) {
index_t v = M.facets.vertex(f,lv);
// .. do something with f,v
}
}If you want a function that works also on polygonal meshes, it works as follows:
for(index_t f=0; f<M.facets.nb(); ++f) {
for(index_t lv=0; lv<M.facets.nb_vertices(f); ++lv) {
index_t v = M.facets.vertex(f,lv);
// .. do something with f,v
}
}Internally, a surfacic mesh is stored as a matrix in CRS (Compressed Row Storage) format. It is also possible to traverse it as follows:
for(index_t f=0; f<M.facets.nb(); ++f) {
for(index_t c = M.facets.corners_begin(f);
c < M.facets.corners_end(f);
++c
) {
index_t v = M.facet_corners.vertex(c);
// .. do something with f,v
}
}and if you want to know, storage is optimized: for a triangulated
mesh, corners_begin(f) is simply 3*f and corners_end(f) is
3*f+3. For a mesh with arbitrary polygons, it is stored explicitly.
One can test whether optimized triangles storage is used with the
function M.facets.are_simplices() (that returns true for a
triangulated mesh, with implicit corners_begin(),corners_end()).
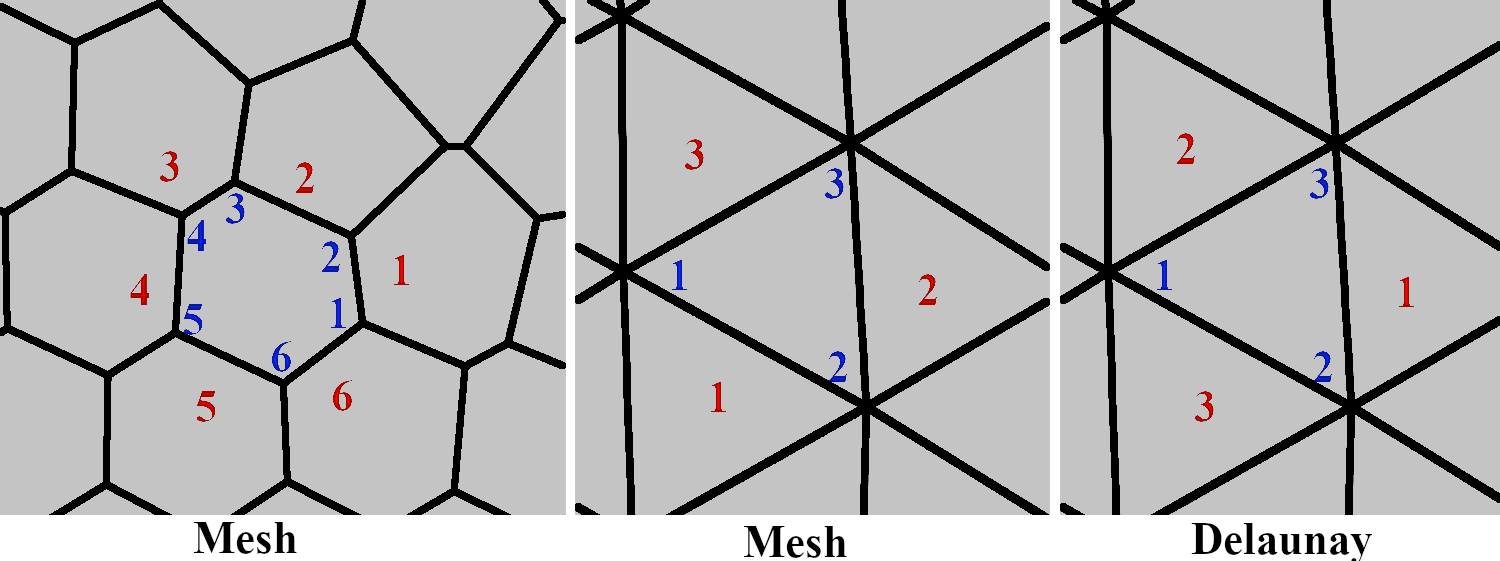
The Mesh data structure also stores facet adjacency information,
that is, for each edge le of a facet f, one can query the facet
adjacent to f along le using M.facets.adjacent(f,le). Edges
are numbered as shown in the figure above: the edge k connects
vertex k to vertex (k + 1) modulo d where d denotes the number
of vertices of the facet. There is a catch when you work with Mesh
and Delaunay in the same code: Delaunay takes a different
convention: edge e is opposite to vertex e (right figure, edge
indices in red, vertices indices in blue). Hence
convention taken for Mesh is different (center and left figures). The
reason is that Delaunay and Mesh have different design constraints:
-
Mesh: needs to work for triangles and arbitrary polygons -
Delaunay: needs to work for simplices of arbitrary dimension (triangles, terahedra, hyper-tetrahedra...)
Halfedge is a popular data structure for meshes. We do not use it for multiple reasons:
- halfedges use much more memory as compared to our arrays, and Geogram is meant to support large meshes, for applications in cosmology for instance
- incidence array is what is used in most file formats, saving a mesh is trivial, and loading it just requires to reconstruct adjacency
- copying a mesh is trivial when using arrays
- storing attributes is just a matter of adding a couple of arrays (more on this below)
- displaying a mesh is just a matter of sending the vertex and incidence arrays to the GPU
- code parallelization is easier and more efficient for loops operating on plain arrays than for pointer-based data structures.
However, using incidence and adjacency arrays, we lose an advantage of Hafledge:
- some operations (for instance, traversing the border) are easier to implement using Halfedge.
For this reason, there is a
geogram/mesh/mesh_halfedges.h
"emulation layer" that provides halfedge-like access to a Mesh.
Another argument for Halfedge is the following one:
- with a halfedge-based data structure, creating and deleting an
element (vertex, halfedge or facet) takes constant time (
O(1))
Clearly, with an array-based data structure, deleting an arbitrary
element takes O(n) (because if the element is in the middle of the
array, this leaves a hole that one needs to shift by shifting the elements
that are after the hole to fill it, which takes n/2 operations in
average), but the point is that deleting a single element is not the
right granularity: in our Mesh data structure, the elementary
operations deletes a set of elements, as follows:
M.vertices.delete_elements(vertices_to_delete);where vertices_to_delete is a vector<index_t> of size
M.vertices.nb() (number of vertices) with its entries set
to 0 for vertices to keep and 1 for vertices to delete.
Internally it computes the permutations to be applied to the
arrays and applies them, which takes O(n).
The same function exists for mesh facets (and also for mesh cells, more on this below):
M.facets.delete_elements(facets_to_delete, delete_isolated_vertices);where facets_to_delete is a vector<index_t> of size
M.facets.nb(). The second argument of the function is a boolean,
if set to true (which is the default), then dangling vertices (with
no facet incident to them) are deleted as well.
This design choice (incidence and adjacency arrays instead of halfedges) is discussed in this keynote Eurographics presentation.

Geogram's Mesh data structure can also store volumetric cells. The
volumetric part of the Mesh can share the same vertices as the
surfacic part, and some file formats (.mesh,.geogram) support
meshes with both surfacic and volumetric information.
Volumetric meshes have a collection of cells, that can be accessed
through M.cells:
-
M.cells.nb(): as you have guessed, returns the number of cells -
M.cells.type(c): wherecis a cell index between0andM.cells.nb()-1, returns the type of the cell, that is, one ofMESH_TET,MESH_HEX,MESH_PRISM,MESH_PYRAMIDandMESH_CONNECTOR -
M.cells.nb_vertices(c),M.cells.vertex(c,lv): query cell indicence -
M.cells.nb_facets(c),M.cells.adjacent(c,lf): query cell adjacency -
M.cells.facet_nb_vertices(c,lf),M.cells.facet_vertex(c,lf,lv): query cell indicence by local facet index and local vertex index in facet.
Internally, Mesh stores cell incidence (cell to vertex relations) in
M.cell_corners, and cell adjacency (cell to cell relations) in
M.cell_facets, with a sparse matrix CRS (compressed row storage) similar to
what is used for polygonal meshes. A Mesh can be made of an arbitrary
mixture of tetrahedra, hexahedra, prisms and pyramids. There is an
additional type of cell (MESH_CONNECTOR) used to represent
non-conformal hybrid meshes where two triangular facets can be
connected to a quadrangular facet.
For tetrahedral meshes, storage is optimized and CRS cell pointers
array is not stored. One can determine if optimized storage is used
with M.cells.are_simplices() (that returns true for a tetrahedral
mesh).
Important mesh facets and mesh cells are two completely unrelated things (besides the fact that they share the same vertices): when one can create a volumetric mesh with no surfacic part, one can copy the border of the volumetric mesh to the surfacic part, or one can use the surfacic part to represent internal boundaries or constraints for a meshing algorithm.
In addition to facets and cells, Mesh can store a set of edges.
Edges can be accessed through M.edges. One can query the two vertices of an edge
using the function M.edges.edge_vertex(e,lv)
where e is an edge between 0 and M.edges.nb()-1, and lv a local vertex
index in {0,1}. Similarly to what was said in the previous paragraph, mesh edges
are completely unrelated with the surfacic and volumetric parts of the mesh. For instance,
one can use them to tag the sharp edges in a surface, or line constraints in constrained Delaunay
triangulation.
Geogram's Mesh has a generic attribute system, that lets one attach objects of arbitrary types
to elements of a mesh. This can be used to store physical properties (pressure, temperature, ...)
in physical simulations, or graphic attributes (colors, texture coordinates, ...) in visualization,
or anything else. Geogram's native file format for meshes (.geogram) stores all the attributes
attached to a mesh. In addition, the attribute system can be extended to new user-defined types.
Geogram attributes can be attached to everything in a mesh that has an index, this includes:
- Vertices
- Edges
- Facets
- Facet corners (that is, a vertex seen from a facet, or a facet edge seen from a facet)
- Cells
- Cell corners (that is, a vertex seen from a cell)
- Cell facets (that is, a facet cell seen from a cell)
One can create and access attributes using the Attribute<T> template, declared in geogram/attributes.h.
Attribute<double> density(M.vertices.attributes(), "density");
for(index_t v=0; v<M.vertices.nb(); ++v) {
density[v] = ...;
}The constructor of Attribute connects to the attribute stored in the
Mesh if it already exists, or creates it if did not exist before. Then
one can manipulate the Attribute as if it was a plain array, indexed
by mesh element index (vertex index in the example above). Attributes
of the following types can be used: Numeric::uint8, char, int,
unsigned int, index_t, signed_index_t, float, double,
vec2, vec3.
advanced In addition, arbitrary types can be used (including
classes that do memory allocation). Before using a new attribute type,
one needs to declare it (only once, at initialization), using
geo_register_attribute_type<type>("name") (see
geogram/common.cpp
for example).
Besides vertices, attribute associated with other
mesh elements can be created using M.edges.attributes(),
M.facets.attributes(), M.facet_corners.attributes(), M.cells.attributes(),
M.cell_corners.attributes() and M.cell_facets.attributes().
The geogram mesh file format (.geogram) saves all the attributes in the file,
one can visualize the result with Vorpaview (more on this below).
One may need to check whether a given attribute exists. This can be done as follows:
Attribute<double> density;
density.bind_if_is_defined(M.vertices.attributes(), "density");
if(!density.is_bound()) {
Logger::err("MyStuff") << "Missing \"density\" vertex attribute"
<< std::endl;
return;
}
...To delete an attribute:
M.vertices.attributes().delete_attribute_store(name);One can also create vector attributes, that associate several values with each
mesh element. In the attribute array, the value of coordinate c associated
with element e is at index dim*e+c, where dim is the dimension of the
vectors:
Attribute<double> vertex_normal;
normals.create_vector_attribute(M.vertices.attributes(),"normal",3);
for(index_t v=0; v<M.vertices.nb(); ++v) {
vec3 N = ...;
vertex_normal[3*v ] = N.x;
vertex_normal[3*v+1] = N.y;
vertex_normal[3*v+2] = N.z;
}One can connect to an existing vector attribute (and check its dimension) as follows:
Attribute<double> vertex_normal;
vertex_normal.bind_if_is_defined(M.vertices.attributes(),"normal");
if(!vertex_normal.is_bound() || vertex_normal.dimension() != 3) {
Logger::err("MyStuff") << "vertex normal attribute is not defined "
<< "or of invalid dimension"
<< std::endl;
return;
}
...Advanced One can assess the underlying continuous array using the
Attribute::data() function. Internally, attributes are stored in a vector<>
(besides a couple of exceptions). One can get a reference to the
underlying vector using the vector<T>& Attribute::get_vector() function.
Before calling it, one can check whether it is supported by an attribute
using the bool Attribute::can_get_vector() function.
The built-in Vorpaview program can visualize surfacic and volumetric meshes,
and the attributes attached to the mesh elements.