notes.md

<style> .{ background-color: black; } h1, h2, h3 { margin-top: 1em; font-weight: bold; color: #ddffff; } strong { color: lightblue; } em { color: #aaccff; } </style>

Visual Perception

Computational Vision

Computational Vision - the process of discovering from images what is present in the world and where. It is challenging because it tries to recover lost information when reversing the imaging process (imperfect imaging process, discretized continuous world)

Applications:

• Automated navigation with obstacle avoidance
• Scene recognition and target detection
• Document processing
• Human computer interfaces

Human Vision

Captured photons release energy which is used as electrical signals for us to see. A photocell in its membrane has ion channels through which ions can flow out. As the light interacts with cell's rhodopsins (type of receptor), the ion channels close and a build-up of electrons occurs in the cell. Such negative charge is captured as an electrical signal by the nerve.

Rod cells (120m) are responsible for vision at low light levees, cones (6m) are active at higher levels and are capable of color vision and have high spatial acuity. There's a 1-1 relationship of cones and neurons so we are able to resolve better, meanwhile many rods converge to one neuron.

Pupils dilate to accept as much light as needed to see clearly.

Receptive field - area on which light must fall for neuron to be stimulated. A receptive field of a Ganglion cell is formed from all photoreceptors that synapse with it.

Ganglion cells - photocells located in retina that process visual information that begins as light entering the eye and transmit it to the brain. There are 2 types of them.

• On-center - fire when light is on center
• Off-center - fire when light is somewhere around center

Ganglion cells allow transition of information about contrast. The size of the receptive field controls the spatial frequency information (e.g., small ones are stimulated by high frequencies for fine detail). Ganglion cells don't work binary (fire/not fire), the change the firing rate when there's light.

Trichromatic coding - any color can be reproduced using 3 primary colors (red, blue, green).

Retina contains only 8% of blue cones and equal proportion of red and green ones - they allow to discriminate colors 2nm in difference and allow to match multiple wavelengths to a single color (does not include blending though)

Optic Physics

Wave frequency $f$ (Hz) and energy $E$ (J) can be calculated as follows ($h=6.623\times 10^{34}$ - Plank's constant, $c=2.998\times 10^8$ - speed of light):

$$f=\frac{c}{\lambda}$$

$$E=hf$$

Perceivable electromagnetic radiation wavelengths are within 380 to 760 nm

Law of Geometric Optics:

1. Light travels in straight lines
2. Ray, its reflection and the normal are coplanar
3. Ray is refracted when it transits medium

Snell's Law - wave crests cannot be created or destroyed at the interface, so to make the waves match up, the light has to change the direction. I.e., given refraction indices $n_1$ and $n_2$, and "in" and "out" angles $\alpha_1$ and $\alpha_2$, there is a relation: $n_1 \sin \alpha_1=n_2 \sin \alpha_2$

Focal length $f$ (m) - distance from lens to the point $F$ where the system converges the light. The power of lens (how much the lens reduces the real world to the image in plane) is just $\frac{1}{f}$ (D) (~59D for human eye)

If the image plane is curved (e.g., back of an eye), then as the angle from optical center to real world object $\tan\theta=\frac{h}{u}=\frac{h'}{v}$ gets larger (when it gets closer to the lens), it is approximated worse.

Edge Detection and Filters

Edge Detection

Intensity image - a matrix whose values correspond to pixels with intensities within some range. (imagesc in matlab displays intensity image).

Colormap - a matrix which maps every pixel to usually (most popular are RGB maps) 3 values to represent a single color. They're averaged to convert it to intensity value.

Image - a function $f(x, y)$ mapping coordinates to intensity. We care about the rate of change in intensity in x and y directions - this is captured by the gradien of intensity Jacobian vector:

$$\nabla f(x, y)=\begin{pmatrix}{\partial f} / {\partial x} \ {\partial f} / {\partial y}\end{pmatrix}$$

Such gradient has x and y component, thus it has magnitude and direction:

$$M(\nabla f)=\sqrt{(\nabla_xf)^2+(\nabla_yf)^2}$$

$$\alpha=\tan^{-1}\left(\frac{\nabla_yf}{\nabla_xf}\right)$$

Edge detection is useful for feature extraction for recognition algorithms

Detection Process

Edge descriptors:

• Edge direction - perpendicular to the direction of the highest change in intensity (to edge normal)
• Edge strength - contrast along the normal
• Edge position - image position where the edge is located

Edge detection steps:

1. Smoothening - remove noise
2. Enhancement - apply differentiation
3. Thresholding - determine how intense are edges
4. Localization - determine edge location

Optimal edge detection criteria:

• Detecting - minimize false positives and false negatives
• Localizing - detected edges should be close to true edges
• Single responding - minimize local maxima around the true edge

First order Edge Filters

To approximate the gradient at the center point of 2-by-2 pixel area, for change in x - we sum the differences between values in rows; for change in y - the differences between column values. We can achieve the same by summing weighted pixels with horizontal and vertical weight matrices (by applying cross-correlation):

$$W_x=\begin{bmatrix}-1 & 1 \ -1 & 1\end{bmatrix};\ W_y=\begin{bmatrix}1 & -1 \ 1 & -1\end{bmatrix}$$

There are other ways to approximate the gradient (not necessarily at 2-by-2 regions): Roberts and Sobel (very popular):

$$W_x=\begin{bmatrix}1 & 0 \ 0 & -1\end{bmatrix};\ W_y=\begin{bmatrix}0 & -1 \ 1 & 0\end{bmatrix}$$

$$W_x=\begin{bmatrix}-1 & 0 & 1 \ -2 & 0 & 2 \ -1 & 0 & 1\end{bmatrix};\ W_y=\begin{bmatrix}1 & 2 & 1 \ 0 & 0 & 0 \ -1 & -2 & -1\end{bmatrix}$$

After applying filters to compute the gradient matrices $G_x$ and $G_y$, we can calculate the magnitude between the 2 to get the final output: $M=\sqrt{G_x^2 + G_y^2}$. Sometimes it's approximated by magnitude values.

Note that given an intensity image $I$ of dimensions $H\times W$ and a filter (kernel) $K$ of dimensions $(2N+1)\times (2M+1)$ the cross-correlation at pixel $h, w$ is expressed as (odd-by-odd filters are more common as we can superimpose the maps onto the original images we want to compare):

$$(I\otimes K){h,w}=\sum{n=-N}^N\sum_{m=-M}^MI_{h+n,w+m}K_{N+n,M+m}$$

We usually set a threshold for calculated gradient map to distinguish where the edge is. We may also upsample the image to enhance the features.

If we use noise smoothing filter, instead of looking for an image gradient after applying the noise filter, we can take the derivative of the noise filter and then convolve it (because mathematically it's the same):

$$\nabla_x(h\star f)=(\nabla_xh)\star f$$

Second order Edge Filters

We can apply Laplacian Operator - by applying the second derivative we can identify where the rate of change in intensity crosses 0, which shows exact edge.

Laplacian - sum of second order derivatives (dot product):

$$\nabla f=\nabla^2 f=\nabla \cdot \nabla f$$

$$\nabla^2I=\frac{\partial^2I}{\partial x^2}+\frac{\partial^2I}{\partial y^2}$$

For a finite difference approximation, we need a filter that is at least the size of 3-by-3. For change in x, we take the difference between the differences involving the center and adjacent pixels for that row, for change in y - involving center and adjacent pixels in that column. I. e., in 3-by-3 case:

$$(\nabla_{x^2}^2I){h,w}=(I{h,w+1}-I_{h,w}) - (I_{h,w} - I_{h,w-1})=I_{h,w-1}-2I_{h,w}+I_{h,w+1}$$

$$(\nabla_{y^2}^2I){h,w}=I{h-1,w}-2I_{h,w}+I_{h+1,w}$$

We just add the double derivative matrices together to get a final output. Again, we can calculate weights for these easily to represent the whole process as a cross-correlation (a more popular one is the one that accounts for diagonal edges):

$$W=\begin{bmatrix}0 & 1 & 0 \ 1 & -4 & 1 \ 0 & 1 & 0\end{bmatrix};\ W=\begin{bmatrix}1 & 4 & 1 \ 4 & -20 & 4 \ 1 & 4 & 1\end{bmatrix}$$

Noise Removal

We use a uniform filter (e.g., in 3-by-3 case all filter values are $\frac{1}{9}$) to average random noise - the bigger the filter, the more details we lose but the less noise the image has due to its smoothness. More popular filters are Gaussian filters with more weight on middle points. Gaussian filter can be generated as follows:

$$H_{ij}= \frac{1}{2\pi\sigma^2}\exp \left(-\frac{(i-(k+1))^2+(j-(k+1))^2}{2\sigma^2} \right) ; 1 \leq i, j \leq (2k + 1)$$

Laplacian of Gaussian - Laplacian + Gaussian which smoothens the image (necessary before Laplacian operation) with Gaussian filter and calculates the edge with Laplacian Operator

Note the noise suppression-localization tradeoff: larger mask size reduces noise but adds uncertainty to edge location. Also note that the smoothness for Gaussian filters depends on $\sigma$.

Canny Edge Detector

Canny has shown that the first derivative of the Gaussian provides an operator that optimizes signal-to-noise ratio and localization

Algorithm:

1. Compute the image gradients $\nabla_x f = f * \nabla_xG$ and $\nabla_y f = f * \nabla_yG$ where $G$ is the Gaussian function of which the kernels can be found by:
   • $\nabla_xG(x, y)=-\frac{x}{\sigma^2}G(x, y)$
   • $\nabla_yG(x, y)=-\frac{y}{\sigma^2}G(x, y)$
2. Compute image gradient magnitude and direction
3. Apply non-maxima suppression
4. Apply hysteresis thresholding

Non-maxima suppression - checking if gradient magnitude at a pixel location along the gradient direction (edge normal) is local maximum and setting to 0 if it is not

Hysteresis thresholding - a method that uses 2 threshold values, one for certain edges and one for certain non-edges (usually $t_h = 2t_l$). Any value that falls in between is considered as an edge if neighboring pixels are a strong edge.

For edge linking high thresholding is used to start curves and low to continue them. Edge direction is also utilized.

Motion

Scale Invariant Feature Transform

SIFT - an algorithm to detect and match the local features (should be invariant) in images. Invariance Types (and how to achieve them):

• Illumination - luminosity changes (solved by difference-based metrics)
• Scale - image size change, magnification change (solved by pyramids, scale space)
• Rotation - roll change along the x axis (solved by rotating to the most dominant gradient direction)
• Affine - generalization of rotation, scaling, stretching etc (solved by normalizing through eigenvectors)
• Perspective - changes in view perspective (solved by rigid transform)

Pyramids - average pooling with stride 2 multiple times

Scale Space - apply Pyramids but take DOGs (Differences of Gaussians) in between and keep features that are repeatedly persistent

Visual Dynamics

By analyzing motion in the images, we look at part of the anatomy and see how it changes from subject to subject (e.g., through treatment). This can also be applied to tracking (e.g., monitor where people walk).

Optical flow - measurement of motion (direction and speed) at every pixel between 2 images to see how they change over time. Used in video mosaics (matching features between frames) and video compression (storing only moving information)

There are 4 options of dynamic nature of the vision:

1. Static camera, static objects
2. Static camera, moving objects
3. Moving camera, static objects
4. Moving camera, moving objects

Difference Picture - a simplistic approach for identifying a feature in the image $F(x, y, i)$ at time $i$ as moved:

$$DP_{12}(x,y)=\begin{cases}1 & \text{if }\ |F(x,y,1)-F(x,y,2)|>\tau \ 0 & \text{otherwise}\end{cases}$$

We also need to clean up the noise - pixels that are not part of a larger image . We use connectedness (more info at 1:05):

• 2 pixels are both called 4-neighbors if they share an edge
• 2 pixels are both called 8-neighbors if they share an edge or a corner
• 2 pixels are 4-connected if a path of 4-neighbors can be created from one to another
• 2 pixels are 8-connected if a path of 8-neighbors can be created from one to another

Motion Correspondence

Aperture problem - a pattern which appears to be moving in one direction but could be moving in other directions due to only seeing the local features movement. To solve this, we use Motion Correspondence (matching).

Motion Correspondence - finding a set of interesting features and matching them from one image to another (guided by 3 principles/measures):

1. Discreteness - distinctiveness of individual points (easily identifiable features)
2. Similarity - how closely 2 points resemble one another (nearby features also have similar motion)
3. Consistency - how well a match conforms with other matches (moving points have a consistent motion measured by similarity)

Most popular features are corners, detected by Moravec Operator (paper) (doesn't work on small objects). A mask is placed over a region and moved in 8 directions to calculate intensity changes (with the biggest changes indicating a potential corner)

Algorithm of Motion Correspondence:

1. Pair one image's points of interest with another image's within some distance
2. Calculate degree of similarity for each match and the likelihood
3. Revise likelihood using nearby matches

Degree of similarity $s$ is just the sum of differences of pixels between 2 patches $i$ (at time $t$) and $j$ (at time $t+1$) (of size $N\times N$) and the likelihood is just the normalized vector of weights $w$ (where $\alpha$ - constant):

$$s_{ij}=\sum_{n=1}^{N\times N}(p_i^{(n)}-p_j^{(n)})$$ $$w_{ij}=\frac{1}{1+\alpha s_{ij}}$$

Hough Transform

A point can be represented as a coordinate (Cartesian space) or as a point from the origin at some angle (Polar space). It has many lines going through and each line can be described as a vector by angle and magnitude $w$ from some origin:

$$w=x \cos \theta + y \sin \theta$$

Hough Space - a plane defined by $w$ and $\theta$ which takes points $(x, y)$ in image space and represents them as sinusoids in the new space. Each point in such space $(w, \theta)$ is parameters for a line in the image space.

Hough Transform - picking the "most voted" intersections of lines in the Hough Space which represent line in the image space passing through the original points (sinusoids in Hough Space)

Algorithm:

1. Create $\theta$ and $w$ for all possible lines and initialize 0-matrix $A$ indexed by $\theta$ and $w$
2. For each point $(x, y)$ and its every angle $\theta$ calculate $w$ and add vote at $A[\theta, w]+=1$
3. Return a line where $A&gt;\text{Threshold}$

There are generalized versions for ellipses, circles etc. (change equation $w$). We also still need to suppress non-local maxima

Image Registration & Segmentation

Registration

Image Registration - geometric and photometric alignment of one image to another. It is a process of estimating an optimal transformation between 2 images.

Image registration cases:

• Individual - align new with past image (e.g, rash and no rash) for progress inspection; align similar sort images (e.g., MRI and CT) for data fusion.
• Groups - many-to-many alignment (e.g., patients and normals) for statistical variation; many-to-one alignment (e.g., thousands of subjects with different sorts) for data fusion

Image Registration problem can be expressed as finding transformation $T$ (i.e., parameterized by $\mathbf{p}$) which minimizes the difference between reference image $I$ and target image $J$ (i.e., image after transformation):

$$\mathbf{p}^=\operatorname{argmin}\mathbf{p} \sum{k=1}^K\underbrace{\text{sim}\left(I(x_k), J(T_{\mathbf{p}}(x_k))\right)}_{{\text{similarity function}}}$$

Components of Registration

Entities to match

We may want to match landmarks (control points), pixel values, feature maps or a mix of those.

Type of transform

Transformations include affine, rigid, spline etc. Most popular:

• Rigid - composed of 3 rotations and 3 translations (so no distortion). Transforms are linear and can be 4x4 matrices (1 translation and 3 rotation).
• Affine - composed of 3 rotations, 3 translations, 3 scales and 3 shears. Transforms are also linear and can be represented as 4x4 matrices
• Piecewise Affine - same as affine except applied to different components (local zones) of the image, i.e., a piecewise transform of 2 images.
• Non-rigid (Elastic) - transforming via 2 forces - external (deformation) and internal (constraints) - every pixel moves by different amount (non-linear).

Similarity function

Conservation of Intensity - pixel-wise MSE/SSD. If resolution is different, we have to interpolate missing values which results in poor similarity

$$\text{MSE}=\frac{1}{K}\sum_{k=1}^K \left(I(x_k) - J(T_{\mathbf{p}}(x_k))\right)^2$$

Mutual Information - maximize the clustering of the Joint Histogram (maximize information which is mutual between 2 images):

• Image Histogram (hist) - a normalized histogram (y - num pixels, x - intensity) representing a discrete PDF where peaks represent some regions.
• Joint Histogram (histogram2) - same as histogram, except pairs of intensities are counted (x, y - intensities, color - num pixel pairs). Sharp heatmap = high similarity.

$$\text{MI}(I,J|T)=\sum_{i\in I}\sum_{j\in J}p(i,j)\log\frac{p(i,j)}{p(i) p(j)}$$

Where $p(i)$ - probability of intensity value $i$ (from image histogram)

Normalized Cross-Correlation - assumes there is a linear relationship between intensity values in the image - the similarity measure is the coefficient ($\bar A$ and $\bar B$ - mean intensity values):

$$CC=\frac{1}{N}\frac{\sum_{i\in I}(A(i)-\bar A)(B(i)-\bar B)}{\sqrt{\sum_{i\in I}(A(i)-\bar A)^2\sum_{i\in I}(A(i)-\bar A)^2}}$$

$$CC=\frac{\text{Cov}[A(i), B(i)]}{\sigma[A(i)]\sigma[B(i)]}$$

More details: correlation, normalized correlation, correlation coefficient, covariance vs correlation, correlation as a similarity measure

Segmentation

Image Segmentation - partitioning image to its meaningful regions (e.g., based on measurements on brightness, color, motion etc.). Non-automated segmentation (by hand) require expertise; Automated segmentation (by models) are currently researched

Image representation:

• Dimensionality: 2D (x, y), 3D (x, y, z), 3D (x, y, t), ND (x, y, z, b2, ..., bn)
• Resolution: spatial (pixels/inch), intensity (bits/pixel), time (FPS), spectral (bandwidth)

Image characterization:

• As signals: e.g., frequency distribution, signal-to-noise-ratio
• As objects: e.g., individual cells, parts of anatomy

Segmentation techniques

• Region-based: global (single pixels - thresholding), local (pixel groups - clustering, PCA )
• Boundary-based: gradients (finding contour energy), models (matching shape boundaries)

Semi-Automated Segmentation

Thresholding

Thresholding - classifying pixels to "objects" or "background" depending on a threshold $T$ which can be selected from image histogram dips. If the image is noisy, threshold can be interactive (based on visuals), adaptive (based on local features), Otsu

Otsu threshold - calculating variance between 2 objects for exhaustive number of thresholds and selecting the one that maximizes inter-class intensity variance (biggest variation for 2 different objects and minimal variation for 1 object)

Smoothing the image before selecting the threshold also works. Mathematical Morphology techniques can be used to clean up the output of thresholding.

Mathematical Morphology

Mathematical Morphology (MM) - technique for the analysis and processing of geometrical structures, mainly based on set theory and topology. It's based on 2 operations - dilation (adding pixels to objects) and erosion (removing pixels from objects).

An operation of MM deals with large set of points (image) and a small set (structuring element). A structuring element is applied as a convolution to touch up the image based on its form.

Applying dilation and erosion multiple times lets to close the holes in segments

Active Contours

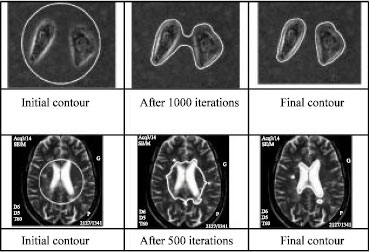
Active Contours - energy minimization problem where we want to find the equilibrium (lowest potential) of the three terms:

• $(E_{int})$ Internal - sensitivity to the amount of stretch in the curve (smoothness along the curve)
• $(E_{img})$ Image - correspondence to the desired image features, e.g., gradients, edges, colors
• $(E_{ext})$ External - user defined constraints/prior knowledge over the image structure (e.g., starting region)

$$E[C(p)]=\alpha \int_0^1 E_{int}[C(p)]dp + \beta \int_0^1 E_{img}[C(p)]dp + \gamma \int_0^1 E_{ext}[C(p)]dp$$

Energy in the image is some function of the image features; Snake is the object boundary or contour

Watershed

Watershed Segmentation - classifying pixels to 3 classes based on thresholding: local minima (min value of a region), catchment basin (object region), watershed (object boundary)

Active Contours

Watershed

3D Imaging

For 3D imaging many images are collected to construct a smooth 3D scene. It is used in archeology (sharing discoveries), industrial inspection (verifying product standard), biometrics (recognizing 3D faces vs photos), augmented reality (IKEA app)

3D imaging is useful because it can remove the necessity to process low level features of 2D images: removes effects of directional illumination, segments foreground and background, distinguishes object textures from outlines

Depth - given a line on which the object exists, it is the shortest distance to the line from the point of interest

Passive Imaging

Passive Imaging - we are concerned with the light that reaches us. 3D information is acquired from a shared field of view (units don't interfere!)

Environment may contain shadows (difficult seeing), reflections (change location of different views = fake correspondences), don't have enough surface features

Stereophotogrammetry

Surface is observed from multiple viewpoints simultaneously. Unique regions of the scene are found in all pictures (which can differ based on perspective) and the distance to the object is calculated considering the dispersity.

Difficult to find pixel correspondence

Structure from motion

Surface is observed from multiple viewpoints sequentially. A single camera is moved around the object and the images are combined to construct an object representation.

If illumination, time of the day, cameras are changing, there is more sparsity

Depth from focus

Surface is observed from different focuses based on camera's depth-of-field (which depends on the lens of the camera and the aperture). The changes are continuous. A focal stack can be taken and a depth map can be generated (though quite noisy).

Difficult to get quantitative numbers. Also mainly sharp edges become blurry when camera is not in focus but not everything has sharp edges

Stereophotogrammetry

Structure from motion

Depth from focus

Active Imaging

Active Imaging - we use the light that we control. It robustly performs dense measurements because little computation is involved, just direct measurements.

Light can be absorbed by dark surfaces and reflected by specular surfaces causing no signal, also multiple units may interfere with each other

Active stereophotogrammetry

Infrared light is used to project surface features and solve the problem of "not enough surface features". Since there is more detail from different viewpoints and since we don't care about patterns (only features themselves), it is easier to find correspondences

Lack of detail produces holes and error depends on distance between cameras. Also, projector brightness decreases with distance therefore things far away cannot be captured.

Time of flight

Distance from the object is found by the time taken for light to travel from camera to the scene. Directional illumination is used to focus photon shooting at just one direction which restricts the view area. Two devices are used:

• Lidar - has a photosensor and a laser pulse on the same axis which is rotated and each measurement is acquired through time. It is robust, however hard to measure short distances due to high speed of light; also is large and expensive.
• Time of flight camera - can image the scene all at once. It uses a spatially resolved sensor which fires light waves instead of pulses and each light wave is recognized by its relative phase. It is fast but depth measure depends on wave properties.

Structured light imaging

To save hardware resources, a projector and a camera are used at different perspectives (unlike in time of flight where they were on the same diagonal). Projected patterns give more information because they can encode locations onto the surface.

• Point scanner (1D) - the position and the direction of the laser is checked and it is calculated where the intersection occurs in the image taken by camera. It is slow because for every point there has to be an image.
• Laser line scanner (2D) - a plane is projected which gives information about the curve of the surface. The depth is then calculated for a line of points in a single image. It is faster but not ideal because image is still not measured at once.

This technique is more accurate (especially for small objects), however the field of view is reduced and there is more complexity in imaging and processing time. Useful in industries where object, instead of laser, moves.

It is time-consuming to move one stripe over time, instead multiple stripes can be used to capture all the object at once. However, if the stripes look the same, camera could not distinguish their location (e.g., if one stripe is behind an object). Time multiplexing is used.

Time multiplexing - different patterns of stripes (arrangements of binary stripes) are projected and their progression through time (i.e., a set of different projections) is inspected to give an encoding of each pixel location in a 3D space.

• For example, in binary encoding, projecting 8 different binary patterns of black | white, i.e., [bw, bwbw, $\cdots$, bwbwbwbw], onto an object, for every resolution point would give an encoding of 8 bits, each bit representing 1 or 0 for the stripe it belongs to at every pattern. There are $2^8$ ways to arrange these bits giving a total of 256 single pixel values.
• Hamming distance - a metric for comparing 2 binary data (sum of digits of a difference between each bit), for instance, the distance between $4$ (0100) and $14$ (1110) is $2$, whereas between $4$ (0100) and $6$ (0110) is $1$
• Given that Grey Code has a Hamming distance of 1 and Inverse Grey Code has a Hamming distance of N-1, progression binary encodings belong to neither category. This means a lot of flexibility and a variety of possible algorithms.

In time multiplexing, because of the lenses, defocus may occur which mangles the edges and, because of the high frequency, information about regions could be lost. Sinusoidal patterns are used which are continuous and less affected by defocus.

Sinusoidal patterns - patterns encoded by a geometric function ($\sin(2\pi f \phi) + 1) / 2$ which has a frequency and a phase which encodes a pixel location. They work as time of flight cameras - the longer the waves (lower $f$), the larger the range, but more noise.

Reconstructing the surface from the wave patterns can cause ambiguities if surface is discontinuous so waves either have to be additionally encoded (labeled) or frequency should be dynamic (low $\to$ high)

Photometric stereo

The goal is to calculate the orientation of the surfaces, not the depth - only the lighting changes, the location and perspective stays the same. If an absolute location of one point in the map is known, with integration other location can be found. LED illumination is used.

• Lambertian reflectance - depends on the angle $\theta$ between the surface normal and the ray to light
• Specular reflectance - depends on the angle $\alpha$ between reflected ray to light and ray to observer

For simplicity, we assume there is no specular reflectance (that surface normal doesn't depend on it). We also assume light source is infinitely far away (constant) The diffusive illumination for each $i^{th}$ light source can be calculated as:

$$I_d=I_pk_d(\mathbf{l}_i \cdot \mathbf{n})$$

Where:

• $\mathbf{l}_i$ - direction to light from surface

• $\mathbf{n}$ - surface normal (different for each pixel)

• $k_d$ - constant reflectance

• $I_p$ -constant light spread

Assuming $\rho=I_pk_d$ and vectorizing the light sources, after some rearrangement we can estimate the surface normal as (knowing $\mathbf{n}$ at each pixel and a some starting point (integration constant), integration is the possible):

$$\rho\mathbf{n}=(L^{\top}L)^{-1}L^{\top}\mathbf{i}$$

Photometric stereo requires many assumptions about illumination and surface reflectance also a point of reference, also precision is no guaranteed because depth is estimated from estimated surface normals

Lidar

Structured light imaging

Photometric stereo

Data Representation

Surface reconstruction

After acquiring a depth map, it is converted (based on the pose and the optics of the camera) to point cloud which contains locations in space for each 3D point. Their neighborhoods help estimate surface normals which are used to build surfaces.

Poisson surface reconstruction - a function where surface normals are used as gradients - inside shape is annotated by ones, outside by zeros. It is a popular function to reconstruct surfaces from normals. It helps to create unstructured meshes.

Surface registration

Knowing a scene representation at different timesteps, they can be combined into one scene via image registration. A model of the scene is taken and its point cloud representations and the best fit is found. If point correspondences are missing, they are inferred. Once all points are known, Kabsch algorithm is applied to find the best single rigid transformation which optimizes the correspondences.

Kabsch algorithm - given 2 point sets $P$ and $Q$, the distance between points in one set and the transformed points in the other set are being minimized: $\min_{R,t}||\mathbf{p}_i-(R\mathbf{q}_i+\mathbf{t})||_2^2$

Point inferring can be done in multiple ways, a simplest one is via iterative closest point where closest points in each set are looked for and the best transformation to reach those points is performed iteratively until the points match.

Face Recognition with PCA

PCA

PCA - algorithm that determines the dominant modes of variation of the data and projects the data onto the coordinate system matching the shape of the data.

Covariance - measures how much each of the dimensions vary with respect to each other. Given a dataset $D={\mathbf{x_1},...,\mathbf{x_N}}$, where $\mathbf{x_N}\in\mathbb{R}^{D}$, the variance of some feature in dimension $i$ and the covariance between a feature in dimension $i$ and a feature in dimension $j$ can be calculated as follows:

$$Var[x_i]=E[(x_i-E[\mathbf{x}_i])^{2}]$$

$$Cov[x_i, x_j]=\Sigma_{x_i, x_j}=E[(x_i - E[\mathbf{x}_i])(x_j - E[\mathbf{x}_j])]$$

Covariance matrix has variances on the diagonal and cross-covariances on the off-diagonal. If cross-covariances are 0s, then neither of the dimensions depend on each other. Given a dataset $D={\mathbf{x_1},...,\mathbf{x_N}}$, where $\mathbf{x_N}\in\mathbb{R}^{D}$, the dataset covariance matrix can be calculated as follows:

$$Var[D]=\Sigma=\frac{1}{N}\sum_{n=1}^N(\mathbf{x}_i-E[D])(\mathbf{x}_i-E[D])^{\top}=(D-E[D])(D-E[D])^{\top}$$

• Identical variance - the spread for every dimension is the same
• Identical covariance - the correlation of different dimensions is the same

PCA chooses such $d^{th}$ columns for $W$ that maximize the variances of projected (mean subtracted) vectors and are orthogonal to each other (meaning information is completely different).

$$\tilde Y = Y - \bar Y$$

$$Var[\tilde Y \mathbf{w}]=(\tilde Y\mathbf{w})^{\top}\tilde Y \mathbf{w}=\mathbf{w}^{\top}\Sigma\mathbf{w}$$

PCA thus becomes an optimization problem constrained to $\mathbf{w}^{\top}\mathbf{w}=\mathbf{1}$ (so that the norm would not go to infinity). Finding the gradient and setting it to 0 shows that the columns of $W$ are basically eigenvectors of the covariance matrix $\Sigma$ of high dimensional space $Y$.

$$\mathcal{F}=\arg\max_{\mathbf{w}}(\mathbf{w}^{\top}\Sigma\mathbf{w} - \lambda(\mathbf{w}^{\top}\mathbf{w}-\mathbf{1}))$$

$$\Sigma\mathbf{w}=\lambda\mathbf{w}$$

In general, the optimization solution for covariance matrix $\Sigma$ will provide $M$ eigenvectors $\begin{bmatrix}\mathbf{w}_1 & \cdots & \mathbf{w}_M\end{bmatrix}$ and $M$ eigenvalues $\begin{bmatrix}\lambda_1 & \cdots & \lambda_M\end{bmatrix}$. The eigenvectors are the principal components of $Y$ ordered by eigenvalues.

PCA works well for linear transformation however it is not suitable for non-linear transformation as it cannot change the shape of the datapoints, just rotate them.

Singular Value Decomposition - a representation of any $X\in\mathbb{R}^{M\times N}$ matrix in terms of the product of 3 matrices:

$$X=UDV^{\top}$$

Where:

• $U\in\mathbb{R}^{M\times M}$ - has orthonormal columns (eigenvectors)
• $V\in\mathbb{R}^{N\times N}$ - has orthonormal columns (eigenvectors)
• $D\in\mathbb{R}^{M\times N}$ - diagonal matrix and has singular values of $X$ on its diagonals ($s_1&gt;s_2&gt;...&gt;0$) (eigenvalues)

In the case of images $\Sigma$ would be $N\times N$ matrix where $N$ - the number of pixles (e.g., $256\times 256=65536$). It could be very large therefore we don't explicitly compute covariance matrix.

Face Recognition

Eigenface - a basis face which is used within a weighted combination to produce an overall face (represented by x - eigenface indices and y - eigenvalues (weights)). They are stored and can be used for recognition (not detection!) and reconstruction.

To compute eigenfaces, all face images are flattened and rearranged as a 2D matrix (rows = images, columns = pixels). Then the covariance matrix and its eigenvalues are found which represent the eigenfaces. Larger eigenvalue = more distinguishing.

Recognition

To map image space to "face" space, every image $\mathbf{x}_i$ is multiplied by every eigenface $\mathbf{v}_k$ to get a respective set of weights $\mathbf{w}_i$:

$$\mathbf{w}_i=\begin{bmatrix}(\mathbf{x}_i-\bar{\mathbf{x}})^{\top}\mathbf{v}_1 & \cdots & (\mathbf{x}_i-\bar{\mathbf{x}})^{\top}\mathbf{v}_K\end{bmatrix}^{\top}$$

Given a weight vector of some new face $\mathbf{w}_{\text{new}}$, it is compared with every other vector based on euclidean distance $d$:

$$d(\mathbf{w}{\text{new}}, \mathbf{w}{i})=||\mathbf{w}{\text{new}} - \mathbf{w}{i}||_2$$

Note that the data must be comparable (same resolution) and size must be reasonable for computational reasons

Medical Image Analysis

Ultraviolet Techniques

Thermography - imaging of the heat being radiated from an object which is measured by infrared cameras/sensors. It helps to spot increased blood flow and metabolic activity when there is an inflammation (detects breast cancer, ear infection).

X-Ray

Process of taking an x-ray photo: A lamp generates electrons which are bombarded at a metal target which in turn generates high energy photons (x-rays). They go though some medium (e.g., chest) and those which pass though are captured on the other side what results in a black | white image (e.g., high density (bones) = white, low density (lungs) = black)

X-ray photos are good to determine structure but we cannot inspect depth

Computed Tomography (CT)

Process of 3D reconstruction via computed tomography (CT): An x-ray source is used to perform multiple scans across the medium to get multiple projections. The data is then back-projected to where the x-rays travelled to get a 3D representation of a medium. In practice filtered back-projections are used with smoothened (convolved with a filter) projected data.

CT reconstructions are also concerned with structural imaging

Nuclear Medical Imaging

Process of nuclear medical imaging via photon emission tomography (PET): A subject is injected with radioactive tracers (molecules which emit radioactive energy) and then gamma cameras are used to measure how much radiation comes out of the body. The detect the position of each gamma ray and back-projection again is used to reconstruct the medium.

Nuclear Imaging is concerned with functional imaging and inspects the areas of activity. However, gamma rays are absorbed in different amounts by different tissues, therefore, it is usually combined with CT

X-Ray Scans

CT Scan Process

PET Scan Process

Other Techniques

Ultrasound Imaging

Ultrasound - a very high pitched sound which can be emitted to determine location (e.g., by bats, dolphins). Sonar devices emit a high pitch sound, listen for the echo and determine the distance to an object based on the speed of sound.

Process of ultrasound imaging using ultrasound probes: An ultrasound is emitted into a biological tissue and the reflection timing is detected (different across different tissue densities) which helps to work out the structure of that tissue and reconstruct its image.

The resolution of ultrasound images is poor but the technique is harmless to human body

Light Imaging

Process of light imaging using pulse oximeters: as blood volume on every pulse increases, the absorption of red light increases so the changes of the intensity of light can be measured through time. More precisely, the absorption at 2 different wavelengths (red and infrared) corresponding to 2 different blood cases (oxy and deoxy) is measured whose ratio helps to infer the oxygen level in blood.

Tissue scattering - diffusion and scattering of light due to soft body. This is a problem because it produces diffused imaging (can't determine from which medium light bounces off exactly (path information is lost), so can't do back-projection)

Several ways to solve tissue scattering:

1. Multi-wavelength measurements and scattering change detection - gives information on how to resolve the bouncing off
2. Time of flight measurements (e.g., by pulses, amplitude changes) - gives information on how far photons have travelled

Process of optical functional brain imaging using a light detector with many fibers: A light travels through skin and bone to reach the surface of the brain. While a subject watches a rotating checkerboard pattern, an optical signal in the brain is measured. Using a 3D camera image registration, brain activity captured via light scans can be reconstructed on a brain model.

Magnetic Resonance Imaging (MRI)

Process of looking at water concentration using magnetic devices: A subject is put inside a big magnet which causes spinning electrons to align with magnetic waves. Then a coil is used around the area of interest (e.g., a knee) which uses radiofrequency - it emits a signal which disrupts the spinning electrons and collects the signal (the rate of it) emitted when the electrons come back to their axes. Such information is used to reconstruct maps of water concentration.

Functional MRI (FMRI) - due to oxygenated blood being more magnetic than deoxygenated blood, blood delivery can be monitored at different parts of the brain based on when they are activated (require oxygenated blood).

MRI is structural and better than CT because it gives better contrast between the soft tissue

Ultrasound imaging

Pulse oximeter

MRI Scanner

Object Recognition

Model Based

Viewpoint-invariant - non-changing features that can be obtained regardless of the viewing conditions. More sensitivity requires more features which is challenging to extract and more stability requires fewer features which are always constant.

Marr's model-based approach on reconstructing 3D scene from 2D information:

1. Primal sketch - understanding what the intensity changes in the image represent (e.g., color, corners)
2. 2.5D sketch - building a viewer-centered representation of the object (object can be recognized from viewer angle)
3. Model selection - building an object-centered representation of the object (object can be recognized from all angles)

Marr's algorithm approaches the problem in a top-down approach (like brain): it observes a general shape (e.g., human), and then if it needs it gets into details (e.g., every human hair). It's object-centered - shape doesn't change depending on view.

Recognition by Components Theory - recognizing objects by matching visual input against structural representations of objects in the brain, consisting of geons and their relations

The problem is that there is an infinite variety of objects so there is no efficient way to represent and store the models of every object. Even a library containing 3D parts (building blocks), would not be big enough and would need to be generalized.

Appearance Based

Appearance based recognition - characterization of some aspects of the image via statistical methods. Useful when a lot of information is captured using multiple viewpoints because an object can look different from a different angle and it may be difficult to recognize using a model which is viewpoint-invariant. A lot of processing is involved in statistical approach.

SIFT can be applied to find features in the desired image which can further be re-described (e.g., scaled, rotated) to match the features in the dataset for recognition (note: features must be collected from different viewpoints in the dataset)

Category Level Recognition

Part Based Model - identifying an object by parts - given a bag of features within the appearance model, the image is checked for those features and determined whether it contains the object. However, we want structure of the parts (e.g., order)

Constellation Model - takes into account geometrical representation of the identified parts based on connectivity models. It is a probabilistic model representing a class by a set of parts under some geometric constraints. Prone to missing parts.

Hierarchical Architecture for object recognition (extract to hypothesize, register to verify):

1. Extract local features and learn more complex compositions
2. Select the most statistically significant compositions
3. Find the category-specific general parts

Appearance based recognition is a more sophisticated technique as it is more general for different viewpoints, however model based techniques work well for non-complex problems because they are very simple.

Robot Vision

Pinhole Camera

Acquiring Image

CMOS | CCD sensor - a digital camera sensor composed of a grid of photodiodes. One photodiode can capture one RGB color, therefore, specific pattern of diodes is used where a subgrid of diodes provides information about color (most popular - Bayer filter).

Bayer fillter - an RGB mask put on top of a digital sensor having twice as many green cells as blue/red to accomodate human eye. A cell represents a color a diode can capture. For actual pixel color, surrounding cells are also involved.

Since depth information is lost during projection, there is ambiguity in object sizes due to perspective

Pinhole Camera

Pinhole camera - abstract camera model: a box with a hole which assumes only one light ray can fit through it. This creates an inverted image on the image plane which is used to create a virtual image at the same distance from the hole on the virtual plane.

Given a true point $=\begin{bmatrix}x & y & z\end{bmatrix}^{\top}$ and a projected point $P'=\begin{bmatrix}x' & y' & z'\end{bmatrix}^{\top}$ (where $z'=f'$ and focal distance is usually given) and that $P'O=\lambda PO$ (beacsue $PO$ and $P'O$ are collinear ($O$ - hole), by similar triangles:

$$\begin{bmatrix}x' & y' & z'\end{bmatrix}^{\top}\to\begin{bmatrix}f'(x/z) & f'(y/z) & f'\end{bmatrix}^{\top}$$

Such weak-perspective projection is used when scene depth is small because magnification $m$ is assumed to be constant, e.g., $x'=-m x$, $y'=-m y$. Parallel projection where points are parallel along $z$ can fix this but are unrealistic.

Pinhole cameras are dark to allow only a small amount of rays hit the screen (to make the image sharp). Lenses are used instead to capture more light.

Camera Geometry

Camera Calibration

Projection of a 3D coordinate system is extrinsic (3D world $\to$ 3D camera) and intrinsic (3D camera $\to$ 2D image). An acquired point in camera 3D coordinates is projected to image plane, then to discretized image. General camera has 11 projection parameters.

For extrinsic projection real world coordinates are simply aligned with the camera's coordinates via translation and rotation:

$$\tilde{X}_{\text{cam}}=R(\tilde{X}-\tilde{C})$$

Homogenous coordinates - "projective space" coordinates (Cartesian coordinates with an extra dimension) which preserve the scale of the original coordinates. E.g., scaling $\begin{bmatrix}x & y & 1\end{bmatrix}^{\top}$ by $w$ (which is usually distance from projector to screen) gives $\begin{bmatrix}wx & wy & w\end{bmatrix}^{\top}$.

In normalized camera coordinate system origin is at the center of the image plane. In the image coordinate system origin is at the corner.

Calibration matrix $K$ - a matrix used to compute projection matrix $P_0$ for a 3D camera coordinate to discrete pixel

$$\begin{pmatrix}x' \ y' \ z'\end{pmatrix}=\underbrace{\begin{bmatrix}\alpha_x & s & x_0 \ 0 & \alpha_y & y_0 \ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0\end{bmatrix}}_{P_0=K \cdot [I|0]}\begin{pmatrix}x \ y \ z \ 1\end{pmatrix}$$

Where:

• $\alpha_x$ and $\alpha_y$ - focal length $f$ (which acts like $z$ (i.e., like extra dimension $w$) to divide $x$ and $y$) multiplied by discretization constant $m_x$ or $m_y$ (which is the number of pixels per sensor dimension unit)
• $x_0$ and $y_0$ - offsets to shift the camera origin to the corner (results in only positive values)
• $s$ - the sensor skewedness: it is usually not a perfect rectangle

Lens adds nonlinearity for which symmetric radial expansion is used (for every point from the origin the radius changes but the angle remains) to un-distort. Along with shear, this transformation is captured in $s$ (see above).

For a general projection matrix, we can obtain a translation vector $\mathbf{t}=-R\tilde{C}$ and write a more general form (assuming homogenousity):

$$X'=K[R|\mathbf{t}]X=PX$$

If 3D coordinates of a real point and 2D coordinates of a projected point are known, then, given a pattern of such points, $P$ can be computed by putting a calibration object in front of camera and determining correspondences between image and world coordinates, i.e., "3D$\to$2D" mapping is solved, e.g., via Direct Linear Transformation (DLT) (see this video) or reprojection error optimization. If positions/orientations are not known, multiplane camera calibration is performed where only many images of a single patterned plane are needed.

Vanishing Points

Given a point $A$ and its direction $D$ towards a vanishing point, any further point is found by $X(\lambda)=A+\lambda D$. If that point is very far, $\lambda=\infty$, $A$ becomes insignificant and projection results in vanishing point itself: $\mathbf{v}=\begin{bmatrix}f x_D/z_D & f y_D / z_D\end{bmatrix}^{\top}$.

Horizon - connected vanishing points of a plane. Each set of parallel lines correspond to a different vanishing point.

Feature-based Alignment

2D Transformation and Affine Fit

Alignment - fitting transformation parameters according to a set of matching feature pairs in original image and transformed image. Several matches are required because the transformation may be noisy. Also outliers should be considered (RANSAC)

Parametric (global) wrapping - transformation which affects all pixels the same (e.g., translation, rotation, affine). Homogenous coordinates are used again to accomodate transformation: $\begin{bmatrix}x' & y' & 1\end{bmatrix}^{\top}=T\begin{bmatrix}x & y & 1\end{bmatrix}^{\top}$. Some examples of $T$:

$$\underbrace{\begin{bmatrix}1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1\end{bmatrix}}{\text{translation}};\ \text{ }\ \underbrace{\begin{bmatrix}s_x & 0 & 0 \ 0 & s_y & 0 \ 0 & 0 & 1\end{bmatrix}}{\text{scaling}};\ \text{ }\ \underbrace{\begin{bmatrix}\cos\theta & -\sin\theta & 0 \ \sin\theta & \cos\theta & 0 \ 0 & 0 & 1\end{bmatrix}}{\text{rotation}};\ \text{ }\ \underbrace{\begin{bmatrix}1 & sh_x & 0 \ sh_y & 1 & 0 \ 0 & 0 & 1\end{bmatrix}}{\text{shearing}}$$

Affine transformation - combination of linear transformation and translation (parallel lines remain parallel). It is a generic matrix involving 6 parameters.

Random Sample Consensus (RANSAC)

RANSAC - an iterative method for estimating a mathematical model from a data set that contains outliers

The most likely model is computed as follows:

1. Randomly choose a group of points from a data set and use them to compute transformation
2. Set the maximum inliers error (margin) $\varepsilon_i=f(x_i, \mathbf{p}) - y_i$ and find all inliers in the transformation
3. Repeat from step 1 until the transformation with the most inliers is found
4. Refit the model using all inliers

In the case of alignment a smallest group of correspondences is chosen from which the transformation parameters can be estimated. The number of inliers is how many correspondences in total agree with the model.

RANSAC is simple and general, applicable to a lot of problems but there are a lot of parameters to tune and it doesn't work well for low inlier ratios (also depends on initialization).

Homography

Homography - projection from plane to plane: $w\mathbf{x}'=H\mathbf{x}$ (used in stitching, augmented reality etc). Projection matrix $H$ can be estimated by applying DLT. It is a mapping between 2 projective planes with the same center of projection.

Stitching - to stitch together images into panorama (mosaic), the transformation between 2 images is calculated, then they are overlapped and blended. This is repeated for multiple images. In general, images are reprojected onto common plane.

For a single 2D point $\begin{bmatrix}wx_i' & wy_i' & w\end{bmatrix}^{\top}=H\begin{bmatrix}x_i & y_i & 1\end{bmatrix}^{\top}$, where $H\in\mathbb{R}^{3\times3}$, every element in the projected point can be weritten as combination of every row element of $H$ and the whole original point, e.g., $wx_i'=H_0\mathbf{x}_i$. With some structuring, a $2 \times 9$ matrix can be created containing values (along with negatives, 1s and 0s) of orignial and projected coordinates and a $9 \times 1$ matrix containing only entries from $H$. Multiplying them would give $2\times 1$ 0s vector. More correspondences can be added which would expand the equation:

$$\underbrace{\begin{bmatrix}x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1'x_1 & -x_1'y_1 & -x_1' \ 0 & 0 & 0 & x_1 & y_1 & 1 & -y_1'x_1 & -y_1'y_1 & -y_1' \ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &\vdots & \vdots & \vdots\ x_N & y_N & 1 & 0 & 0 & 0 & -x_N'x_N & -x_N'y_N & -x_N' \ 0 & 0 & 0 & x_N & y_N & 1 & -y_N'x_N & -y_N'y_N & -y_N' \ \end{bmatrix}}{A}\underbrace{\begin{bmatrix}h{11} \ h_{12} \ h_{13} \ h_{21} \ h_{22} \ h_{23} \ h_{31} \ h_{32} \ h_{33}\end{bmatrix}}{\mathbf{h}}=\underbrace{\begin{bmatrix}0 \ 0 \ \vdots \ 0 \ 0\end{bmatrix}}{\mathbf{0}}$$

This can be formulated as least squares: $\min||A\mathbf{h}-\mathbf{0}||^2$ to which the solution is $\mathbf{h}$ is the eigenvector of $A^{\top}A$ with the smallest eigenvalue (assuming $||\mathbf{h}||^{2}=1$ so that values wouldn't be infinitely small).

During forward wrapping (projection), pixels may be projected between discrete pixels in which case splatting - color distribution among neighboring pixels - is performed. For inverse wrapping, color from neighbors is interpolated.

Local Features

Local Feature Selection

Local features - identified points of interest, each described by a feature vector, which are used to match descriptors in a different view. Applications include image alignment, 3D reconstruction, motion tracking, object recognition etc.

Local feature properties:

• Repeatability - same feature in multiple images (despite geometric/photometric transformations). Corners are most informative
• Saliency - distinct descriptions for every feature
• Compactness - num features $\ll$ image pixels
• Locality - small area occupation

Harris Corner Detector - detects intensity $(I)$ change for a shift $[u, v]$ (weighted auto-correlation; $w(\cdot)$ - usually Gaussian kernel):

$$E(u, v)=\sum_{x,y}\underbrace{w(x, y)}_{\text{weight fn}}[I(x+u,y+v) - I(x,y)]^2$$

For small shifts $E$ can be approximated (Taylor Expansion) as $E(u,v)\approx \begin{bmatrix}u & v\end{bmatrix}M\begin{bmatrix}u & v\end{bmatrix}^{\top}$, where $M\in\mathbb{R}^{2\times 2}$ - a weighted sum of matrices of image region derivatives (covariance matrix), which can be expressed as a convolution with Gaussian filter:

$$M=G(\sigma)*\begin{bmatrix}(\nabla_{x}I)^2 & \nabla_{x}I\nabla_{y}I \ \nabla_{x}I\nabla_{y}I & (\nabla_yI)^2\end{bmatrix}$$

Such $M$ can then be decomposed into eigenvectors $R$ and eigenvalues $\lambda_{min}$, $\lambda_{max}$ (strong eigenvector = strong edge component):

$$M=R\begin{bmatrix}\lambda_{max} & 0 \ 0 & \lambda_{min}\end{bmatrix}R^{\top}$$

If eigenvalues are large, a corner is detected because intensity change (gradient) is big in both $x$ and $y$ directions. But only the ratio and a rough magnitude is checked (calculating eigenvalues is expensive). It's possible because $\det(M)=\lambda_1\lambda_2$ and $\text{trace}(M)=\lambda_1 + \lambda_2$ In practice, Corner Response Function (CRF) is checked against some threshold $t$ (usually $0.04 &lt; \alpha &lt; 0.06$ works):

$$\underbrace{\det(M)-\alpha\text{trace}^2(M)}_{\text{CRF}}>t$$

Non-maxima suppression is applied after thresholding.

Harris Detector is rotation invariant (same eigenvalues if image is rotated) but not scale invariant (e.g., more corners are detected if a round corner is scaled)

Hessian Corner Detector - finds corners based on values of the determinant of the Hessian of a region:

$$\text{Hessian}(I)=\begin{bmatrix}\nabla_{xx}I & \nabla_{xy}I \ \nabla_{xy}I & \nabla_{yy}I\end{bmatrix}$$

Local Feature Detection

Automatic scale selection - a scale invariant function which outputs the same value for regions with the same content even if regions are located at different scales. As scale changes, the function produces a different value for that region and the scales for both images is chosen where the function peaks out:

Blob - superposition of 2 ripples. A ripple is a zerocrossing function at an edge location after applying LoG. Because of the shape of the LoG filter, it detects blobs (maximum response) as spots in the image as long as its size matches the spot's scale. In which case filter's scale is called characteristic scale.

Note that in practice LoG is approximated with a difference of Gaussian (DoG) at different values of $\sigma$. Many such differences form a scale space (pyramid) where local maximas among neighboring pixels (including upper and lower DoG) within some region are chosen as features

Local Feature Description

SIFT Descriptor - a descriptor that is invariant to scale. A simple vector of pixels of some region does not describe a region well because a corresponding region in another image may be shifted causing mismatches between intensities. SIFT Descriptor creation:

1. Calculate gradients on each pixel and smooth over a few neighbors
2. Split the region to 16 subregions and calculate a histogram of gradient orientations (8 directions) at each
3. Each orientation is described by gradient's magnitude weighted by a Gaussian centered at the region center
4. Descriptor is acquired by stacking all histograms (4$\times$4$\times$8) to a single vector and normalizing it

Actually, before the main procedure of SIFT, the orientation must be normalized - the gradients are rotated into rectified orientation. It is found by computing a histogram of orientations (region is rotated 36 times) where the largest angle bin represents the best orientation.

To make the SIFT Descriptor invariant to affine changes, covariance matrix can be calculated of the region, then eigenvectors can be found based on which it can be normalized.

SIFT Descriptor is invariant:

• Scale - scale is found such that the scale invariant function has local maxima
• Rotation - gradients are rotated towards dominant orientation
• Illumination (partially) - gradients of sub-patches are used
• Translation (partially) - histograms are robust to small shifts
• Affine (partially) - eigenvectors are used for normalization

When feature matches are found, they should be symmetric

Multiple-View Geometry

Stereophotogrammetry

Stereo imaging (triangulation) - given several images of the same object, its 3D representation is computed (e.g., depth map, point cloud, mesh etc.)

3D point reconstruction can be calculated by intersection of 2 rays (projection points in the images). In practice, rays will not intersect, therefore linear and non-linear approaches are considered (note: 3D point is unknown but the projection points in the 2 images are known):

1. The former solves a homogenous system by SVD resulting in the desired 3D point being the smallest eigenvector. It generalizes well but has error cases.
2. The latter introduces a reprojection error (mismatch between true and generated projections of a predicted 3D point). True point is detected when the error is minimized. It's very accurate but requires iterative solution.

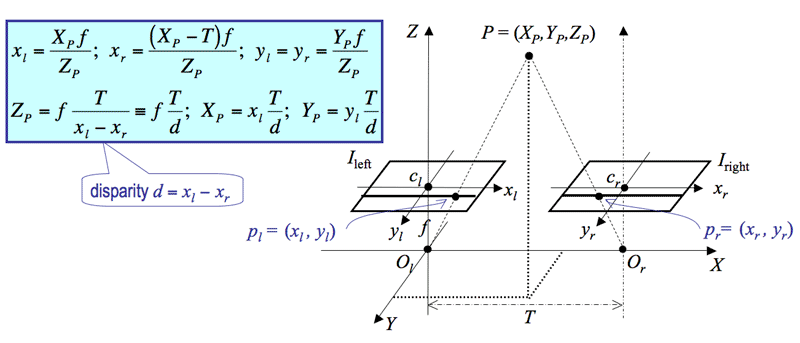
If the correspondence in another image is not known but cameras are in parallel, then given their focal length $f$, distance between their optical centers $T$, distance between the 2 projected points (disparity) $x_l - x_r$, the distance (depth) $Z_p$ to the point can be computed using similar triangles:

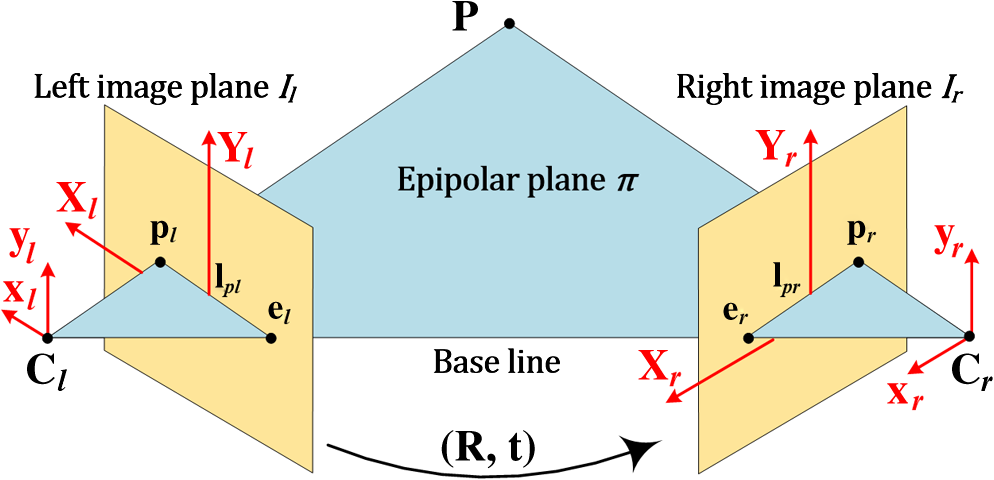
If cameras are not in parallel, disparity won't help, thus epipolar geometry is considered which simplifies the correspondence problem to 1D search along an epipolar line. In one image a ray from the projected point to the 3D point is projected in another image (epipolar line) where we look for a point from which the ray (to the 3D point) would be projected in the initial image crossing its projected point. Connecting those points with epipoles (where base line crosses image plane) results in epipolar plane.

To get an epipolar line when some point is selected on the left image, there has to be some constraints for the stereo system.

If camera calibrations are known, essential matrix $E=T\times R$ can be constructed which relates the corresponding image points (translation cross rotation) and assuming $\mathbf{p}_l$ and $\mathbf{p}_r$ (e.g., $\mathbf{p}_l=\begin{bmatrix}x_l & y_l & f\end{bmatrix}^{\top}$) are rays from camera centers to corresponding points, the following Epipolar Constraint holds (note that vector $(\mathbf{p}l^{\top}E)^{\top}$ represents epipolar line $\mathbf{l}{pr}$ and vector $E\mathbf{p}r$ represents $\mathbf{l}{pl}$):

$$\mathbf{p}_l^{\top}E\mathbf{p}_r=0$$

For a non-calibrated system coordinates cannot be transformed, however by combining left and right cameras' intrinsic parameters $K_l$ and $K_r$, a fundamental matrix can be acquired $F=(K_l^{\top})^{-1}EK_r$. Then $E$ can be substituted by $F$ but instead of image plane coordinates $\mathbf{p}_l$ and $\mathbf{p}_r$, image pixels have to be used (since they are multiplied by $(K_l^{\top})^{-1}$ and $K_r$ to give $\mathbf{p}_l$ and $\mathbf{p}_r$):

$$\mathbf{x}_l^{\top}F\mathbf{x}_r=0$$

If optical axes are parallel stereo image rectification is performed - images are reprojected onto a common plane, parallel to the base line where the depth can be computed based on disparity.

To estimate $F$, we need to collect some good correspondence examples to "reverse engineer" $F$:

• Assumptions: points in both cameras are visible, regions are similar and the baseline is small compared to depth
• Correspondences: once a feature point is selected in one image, a corresponding feature in the other image is checked via dense correspondences - a window is slide through epipolar line and such regions is selected where the cost is the lowest (best similarity)
• Constraints - 1-1 correspondence, same order of points (no in-between objects), locally smooth disparity

Structure from Motion

SFM - reconstruction of camera positions given several images of the same scene

To compute the projection matrix $P_j$, calibration matrix $K_j$, rotation $R_j$ and translation $\mathbf{t}_j$ parameters are required which can be computed from essential matrix $E_j$ which can be computed from fundamental matrix $F_j$. If the camera is moving, the calibration matrices $K_j$ are all the same. $F$ is estimated such that it minimizes the projection errors (note that good initialization is required):

$$\epsilon(F)=\frac{1}{N}\sum_{n=1}^N\left(d^2(\mathbf{x}_l^{(i)}, F\mathbf{x}_r^{(i)}) + d^2(\mathbf{x}_r^{(i)}, F^{\top}\mathbf{x}_l^{(i)})\right)$$

In general correspondences are unknown and they are jointly looked for. The general algorithm for correspondences and $F$:

1. Find key points in the images (e.g., corner)
2. Calculate potential matches
3. Estimate epipolar geometry (use RANSAC)
4. Improve match estimates and iterate

Recognition

Features as Instances

Each local feature region has a descriptor which is a point in a high-dimensional space (e.g., SIFT). An efficient way to perform feature retrieval is to make the problem similar to text retrieval, i.e., indexing. For that, each feature is mapped to tokens/words by quantizing the feature space via clustering (to make a discrete set of "visual words", i.e., bag of words).

Texton - cluster center of filter responses over collection of images. It is assigned to features that are closest to it.

To identify textures (repeated local patterns), filters that look like patterns themselves are used to find them and then local windows are used for statistical description. Textures can be represented by a 2D graph of points representing windows (x - mean $\nabla_x$, y - mean $\nabla_y$). Points can be grouped together under the same texton.

Inverted indexing (each "visual word" is assigned a list of images) is used to enable faster search at query time

Given a fixed set of features, every image can be represented in terms of that set by a distribution of every feature occurrence. Then, given two such representations $d_j$ (desired image) and $q$ (query image), similarity can be calculated:

$$\text{sim}(d_j,q)=\frac{\langle d_j, q\rangle}{||d_j||\ |||q||}$$

Given some query and a database, retrieval quality is calculated by precision (num relevant / tot returned) and recall (num relevant / tot relevant). Obtaining all possible precisions and recalls for a single query forms a PR curve under which the area can be calculated to produce an accuracy score.

For computational efficiency, hierarchical clustering is used to subgroup textons

Bag of words pros and cons:

• (+) Flexible to geometry/deformation
• (+) Compact summary of image content
• (+) Vector representation for sets
• (-) Ignored geometry must be verified
• (-) Mixed foreground and background
• (-) Unclear optimal vocabulary

Instance Recognition

Recognized instances must be spatially verified, e.g., using RANSAC (by checking support for possible transformations) or generalized Hough Transform (by allowing each feature to cast a vote on location, scale and orientation).

Term Frequency - Inverse Document Frequency (TF-IDF) weighting - another way to retrieve query results taken from text retrieval. Such weighting describes frames by their word frequency and downweights words that appear often in the database (aims to retrieve results that have a lot of similarity with the query but overall are as little similar to other documents):

$$t_i=\frac{n_{id}}{n_d}\log\frac{N}{n_i}$$

Where:

• $n_{id}$ - num occurrences of word $i$ in document $d$
• $n_d$ - num words in document $d$
• $n_i$ - num documents word $i$ occurs in
• $N$ - tot num documents in the database

Query Expansion - acquiring filtered query results and reusing them for the same query to obtain even more results

Object Recognition

Object categorization - given a small number of training samples, recognize a priori unknown instances and assign a correct label. There are 2 object categorization levels: instance (e.g., a car) and category (e.g., a bunch of cars). There are also different levels of abstraction: abstract (e.g., animal), basic (e.g., dog), individual (e.g., German Shepard). Basic is most commonly chosen as it reflects humans.

Supervised classification - given a collection of labeled samples, a function is looked for that can predict labels for new samples. The function is good when the risk (expected loss) is minimized. There are 2 models for that:

• Generative - training data is used to build a probability model (conditional densities, priors are modeled) [e.g., CNN]
• Discriminative - a decision boundary is constructed directly (posterior is modeled) [e.g., SVM]

Deep Learning for Computer Vision

Learning types:

• Reinforcement learning - learn to select an action of maximum payoff
• Supervised learning - given input, predict output. 2 types: regression (continuous values), classification (labels)
• Unsupervised learning - discover internal representation of an input (also includes self-supervised learning)

Applications to computer vision:

• Classification - assign class labels to images [ResNet, SENet]
• Detection - identify rectangular regions of objects [Faster R-CNN, YOLO]
• Segmentation - classify each pixel to a specific category [DeepLab, UNet]
• Low-level vision - pixel-based processing techniques (denoising, super-resolution, inpainting etc.)
• 3D vision - 3D/depth reconstruction [NERF]
• Vision + X - processing vision along with other modalities like audio/speech (e.g., DALLE)

Artificial neuron representation:

1. $\mathbf{x}$ - input vector ("synapses") is just the given features
2. $\mathbf{w}$ - weight vector which regulates the importance of each input
3. $b$ - bias which adjusts the weighted values, i.e., shifts them
4. $\mathbf{z}$ - net input vector $\mathbf{w}^{\top}\mathbf{x}+b$ which is linear combination of inputs
5. $g(\cdot)$ - activation function through which the net input is passed to introduce non-linearity
6. $\mathbf{a}$ - the activation vector $g(\mathbf{z})$ which is the neuron output vector

Artificial neural network representation:

1. Each neuron receives inputs from inputs neurons and sends activations to output neurons
2. There are multiple neuron layers and the more there are, the more powerful the network is (usually)
3. The weights learn to adapt to the required task to produce the best results based on some loss function

Popular activation functions - ReLU, sigmoid and softmax, the last two of which are mainly used in the last layer before the error function:

$$\text{ReLU}(x)=\max(0, x);\ \text{ }\ \text{ }\ \text{ }\ \sigma(x)=\frac{1}{1+\exp(-x)};\ \text{ }\ \text{ }\ \text{ }\ \text{softmax}(x)=\frac{\exp(x)}{\sum_{x'\in\mathbf{x}}\exp(x')}$$

Popular error functions - MSE (for regression), Cross Entropy (for classification):

$$\text{MSE}(\hat{\mathbf{y}}, \mathbf{y})=\frac{1}{N}\sum_{n=1}^N(y_n-\hat{y}n)^2;\ \text{ }\ \text{ }\ \text{ }\ \text{ }\ \text{CE}(\hat{\mathbf{y}}, \mathbf{y})=-\sum{n=1}^N y_n \log \hat{y}_n$$

Backpropagation - weight update algorithm during which the gradient of the error function with respect to the parameters $\nabla_{\mathbf{w}}E$ is calculated to find the update direction such that the updated weights $\mathbf{w}$ iteratively would lead to minimized error value.

$$\mathbf{w}\leftarrow \mathbf{w} - \alpha \nabla_{\mathbf{w}} E(\mathbf{w})$$

To avoid overfitting, early stopping, dropout, batch normalization, regularization data augmentation are used. Also data preprocessing, e.g., PCA, normalization

Locally connected layer - neurons which are connected only to local regions of an image instead of all the pixels. This allows less computational resources and limits parameter space allowing less samples for training.

The size of the feature map acquired after convolution depends on the kernel size (filter width/height), padding (border size), dilation (gap size ratio between filter values) and stride (sliding step size):

$$S_{out}=\frac{S_{in} + 2 \times \text{padding} - \text{dilation} \times (\text{kernel_size}-1)-1}{\text{stride}}-1$$

Transfer Learning - if there is not enough data, a majority of the network can be initialized with already learned weights (majority of which can be kept frozen during training) from another network and only the remaining part can be trained.

Modern research topics:

• Generative Adversarial Networks (GANs) - given some input space (created via VAEs), a generator creates an image and a discriminator classifies how real it is. It is a min-max optimization problem. [DCGAN]
• Self-supervised learning - learning from the data itself without labels. There are 2 types: learning specific tasks (labels are within the training samples, e.g., colorizing) and learning general representations (trained on general data, then fine-tuned). Other modalities like audio can also be used to self-supervision.
• Transformers (vision) - multi-head attention module is used which transforms the input data to value, key and query such that they have a high correlation.Image patches are used as tokens to do data fusion.

Practice Questions

1. Visual Perception

   • Why is computational vision challenging? Some applications.
   • How photocell's interaction with light is registered as an electric signal?
   • Difference between rods & cones
   • How Ganglion cells work + types
   • Trichromatic coding + how is color captured in the eye
   • Perceivable electormagnetic wavelengths range
   • Law of Geometric Optics + Snell's Law
   • Focal length of a human eye
   • Lens + Magnification formulas
   • How curved image plane impacts object/image approximation?

2. Edge Filters

   • Intensity image + Colormap + Image
   • How is magnitude and direction computed of a gradient map?
   • Edge descriptors, detection steps and detection criteria
   • How 1st order edge detector works; what are some popular ones?
   • How 2nd order edge detector works; what is a popular operator?
   • What filter is used for noise removal; how can it be created?
   • Noise suppression-localization tradeoff
   • How to combine noise and edge filter into one? Why is it useful?
   • Canny Edge Detection algorithm

3. Motion

   • SIFT and types of invariances
   • Where image motion analysis can be applied?
   • Optical Flow + its usage
   • Difference Picture + usage of connectedness to clean up noise
   • Motion correspondence and its 3 principles + Aperture problem
   • Algorithm for Motion correspondence and what is used for degree of similarity
   • How Hough Transform works?

4. Registration & Segmentation

   • Image Registration and its cases; how it can be expressed mathematically?
   • Types of entities we want to match and transformations we may encounter
   • Conservation of Intensity, Mutual Information and Normalized CC
   • How image segmentation (histogram-based) depends on image resolution?
   • Image segmentation + its techniques
   • Image representation and Image characterization types
   • Thresholding for segmentation + its types (what is Otsu Threshold?)
   • Mathematical Morphology for segmentation, how does it incorporate structuring elements?
   • Active Contours for segmentation, what is energy and snake in the image?
   • Watershed for segmentation

5. 3D Imaging

   • 3D Imaging applications and why is it useful?
   • Passive Imaging and Active Imaging + challenges of each
   • Stereophotogrammetry, Structure from motion and Depth from focus - how it works + challenges
   • How does Active Stereophotogrammetry work + its challenges?
   • Structured light imaging + its 1D and 2D devices
   • Time multiplexing and why we need it?
   • What are sinusoidal patterns used for?
   • Photometric stereo + its challenges.
   • Reflectance types and diffusive illumination formula
   • How does surface reconstruction work + how Poisson function contributes to it?
   • How does surface registration work + how Kabsch algorithm contributes to it?

6. Face Recognition with PCA

   • Variance and Covariance formulas + how to compute Covariance Matrix $\Sigma$?
   • PCA + its algorithm
   • Where PCA is not suitable?
   • PCA expressed as SVD
   • Eigenface + how to compute it + where are they used?
   • Face recognition given a dataset of eigenfaces

7. Medical Image Analysis

   • Thermography and where is it used?
   • How to take an x-ray photo and where is it used?
   • How to perform CT and why do we use it?
   • How does PET work? Is it structural or functional imaging? Why do we combine it with CT?
   • How doe imaging with ultrasound works? What's its advantage?
   • How pulse oximeters work? How is light used for brain imaging? Problem of tissue scattering + how to solve it?
   • How do MRI and FMRI work? Why are they preferred over CT?

8. Object Recognition

   • Viewpoint invariance + sensitivity-stability tradeoff
   • Marr's model-based algorithm + how is it similar to brain?
   • How does recognition by Components Theory works?
   • Problem of model-based object recognition
   • How does appearance-based object recognition works? How SIFT becomes handy?
   • Difference between Part-based model and Constellation Model
   • Hierarchical Architecture for object recognition
   • When o use appearance-based and when to use model-based object recognition?

9. Robot Vision

   1. Camera Geometry
      • How does CMOS/CCD photosensor work along with Bayer Filter?
      • How pinhole cameras work and why are they dark?
      • Weak-perspective projection principle (when depth is small)
      • Difference between intrinsic and extrinsic projection
      • Homogenous coordinates
      • Calibration matrix $K$ (and its parameters) and a general projection matrix (how can it be computed?)
      • Vanishing point and horizon
   2. Alignment & Features
      • Alignment, affine transform + examples of parametric wrapping
      • RANSAC and its algorithm (when it can fail?)
      • Homography and stitching
      • Estimation of projection matrix $H$ as optimization problem
      • Local features and their properties
      • Harris Corner Detector and its approximated expression (by Taylor Series) convolved with Gaussian
      • Corner Response Function and why it is used. How invariant Harris Detector is?
      • Hessian Corner Detector
      • How automatic scale selection works?
      • How are blobs detected and how pyramids are used for feature selection?
      • SIFT Descriptor and how to create it. How invariant is is?
   3. Multiple-View Geometry
      • Stereo imaging; difference between linear and non-linear approach for 3D point reconstruction
      • When and how can disparity be used for depth estimation?
      • When epipolar geometry is used for depth estimation? Terms: epipolar line, epipolar plane, epipole, baseline
      • Why constraints are needed for a stereo system? How to approach them in calibrated and non-calibrated cases?
      • Essential matrix, fundamental matrix and Epipolar Constraint
      • What correspondences to use for estimating $F$?
      • SFM and what projection error is used?
      • Iterative algorithm for estimating $F$
   4. Recognition
      • How feature retrieval is approached via bag of words? Its pros and cons?
      • What is texton and how textures are identified?
      • How to calculate similarity between given and queried images? What is inverted indexing?
      • How to evaluate retrieval accuracy based on precision-recall curve?
      • How does retrieval based on TF-IDF weighting work?
      • Query expansion
      • Object categorization; its level types and abstraction types
      • Supervised classification and its 2 types

10. Deep Learning

    • Deep learning types, applications for CV
    • Artificial neuron and NN representation
    • Popular activation and error functions
    • Backpropagation and how to tackle overfitting?
    • Local connectivity vs global connectivity
    • How to compute feature map size given kernel_size, padding, dilation and stride?
    • Transfer learning
    • 3 modern research techniques for imaging and how they generally work?