According to Wikipedia:
In computer science, a disjoint-set data structure (also called a union–find data structure or merge–find set) is a data structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. It provides near-constant-time operations (bounded by the inverse Ackermann function) to add new sets, to merge existing sets, and to determine whether elements are in the same set. In addition to many other uses (see the Applications section), disjoint-sets play a key role in Kruskal's algorithm for finding the minimum spanning tree of a graph.
MakeSet creates 8 singletons.
After some operations of Union, some sets are grouped together.
The idea of Disjoint Sets can be perfectly applied in finding the minimal spanning tree. The Disjoint Sets consist of two basic operations: finding the group (parent) of any element, unioning two or more sets.
| Operation | Complexity |
|---|---|
| Access | --- |
| Search | O(1) |
| Space | O(n) |
| Merge | O(1) |
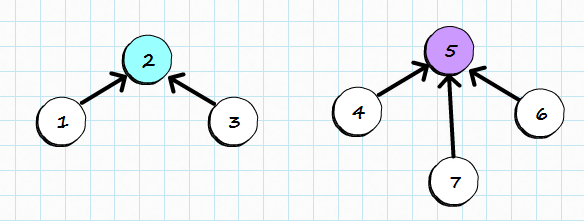
Simple representation of a Disjoint Set
Two sets, one with 3 the other with 4 items
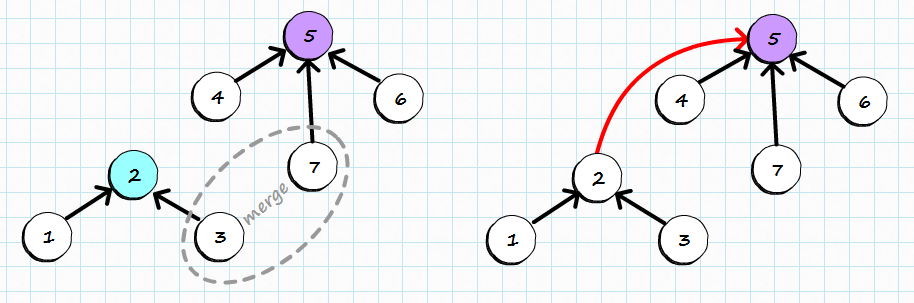
Merging:
Merging sets