b-tree

B-Tree

According to Wikipedia:

In computer science, a B-tree is a self-balancing tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children. Unlike self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as discs. It is commonly used in databases and filesystems.

In a binary search tree, AVL Tree, Red-Black tree etc., every node can have only one value (key) and maximum of two children but there is another type of search tree called B-Tree in which a node can store more than one value (key) and it can have more than two children. B-Tree was developed in the year of 1972 by Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.

B-Tree can be defined as follows: B-Tree is a self-balanced search tree with multiple keys in every node and more than two children for every node.

In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, a B-Tree node size is kept equal to the disk block size. Since h is low for B-Tree, total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, etc.

Properties of B-Tree

1. All leaves are at same level.
2. A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3. Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4. All nodes (including root) may contain at most 2t – 1 keys.
5. Number of children of a node is equal to the number of keys in it plus 1.
6. All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7. B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8. Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(log n).

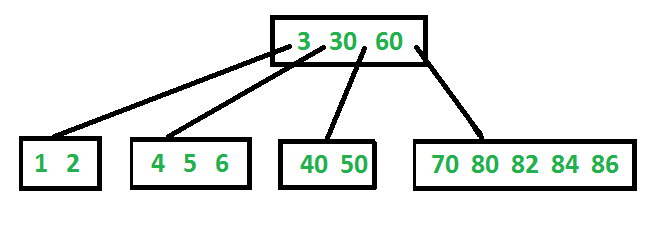
Below is an example B-Tree of minimum degree 3. Note that in practical B-Trees, the value of minimum degree is much more than 3.

Another example, B-Tree of Order 4 contains maximum 3 key values in a node and maximum 4 children for a node.

Operations on a B-Tree

The following operations are performed on a B-Tree:-

1. Search
2. Insertion
3. Deletion

Search

Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.

In a Binary search tree, the search process starts from the root node and every time we make a 2-way decision (we go to either left subtree or right subtree). In B-Tree also search process starts from the root node but every time we make n-way decision where n is the total number of children that node has. In a B-Ttree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows:-

1. Read the search element from the user
2. Compare, the search element with first key value of root node in the tree.
3. If both are matching, then display "Given node found!!!" and terminate the function
4. If both are not matching, then check whether search element is smaller or larger than that key value.
5. If search element is smaller, then continue the search process in left subtree.
6. If search element is larger, then compare with next key value in the same node and repeate step 3, 4, 5 and 6 until we found exact match or comparision completed with last key value in a leaf node.
7. If we completed with last key value in a leaf node, then display "Element is not found" and terminate the function.

Insertion

In a B-Tree, the new element must be added only at leaf node. That means, always the new keyValue is attached to leaf node only. The insertion operation is performed as follows:-

1. Check whether tree is Empty.
2. If tree is Empty, then create a new node with new key value and insert into the tree as a root node.
3. If tree is Not Empty, then find a leaf node to which the new key value cab be added using Binary Search Tree logic.
4. If that leaf node has an empty position, then add the new key value to that leaf node by maintaining ascending order of key value within the node.
5. If that leaf node is already full, then split that leaf node by sending middle value to its parent node. Repeat tha same until sending value is fixed into a node.
6. If the spilting is occuring to the root node, then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Example

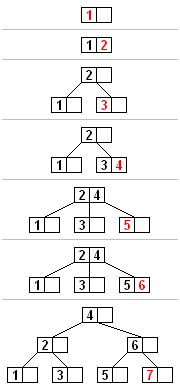
A B Tree insertion example with each iteration. The nodes of this B tree have at most 3 children (Knuth order 3).

Deletion

There are two popular strategies for deletion from a B-tree.

1. Locate and delete the item, then restructure the tree to retain its invariants, OR
2. Do a single pass down the tree, but before entering (visiting) a node, restructure the tree so that once the key to be deleted is encountered, it can be deleted without triggering the need for any further restructuring

The algorithm below uses the former strategy.

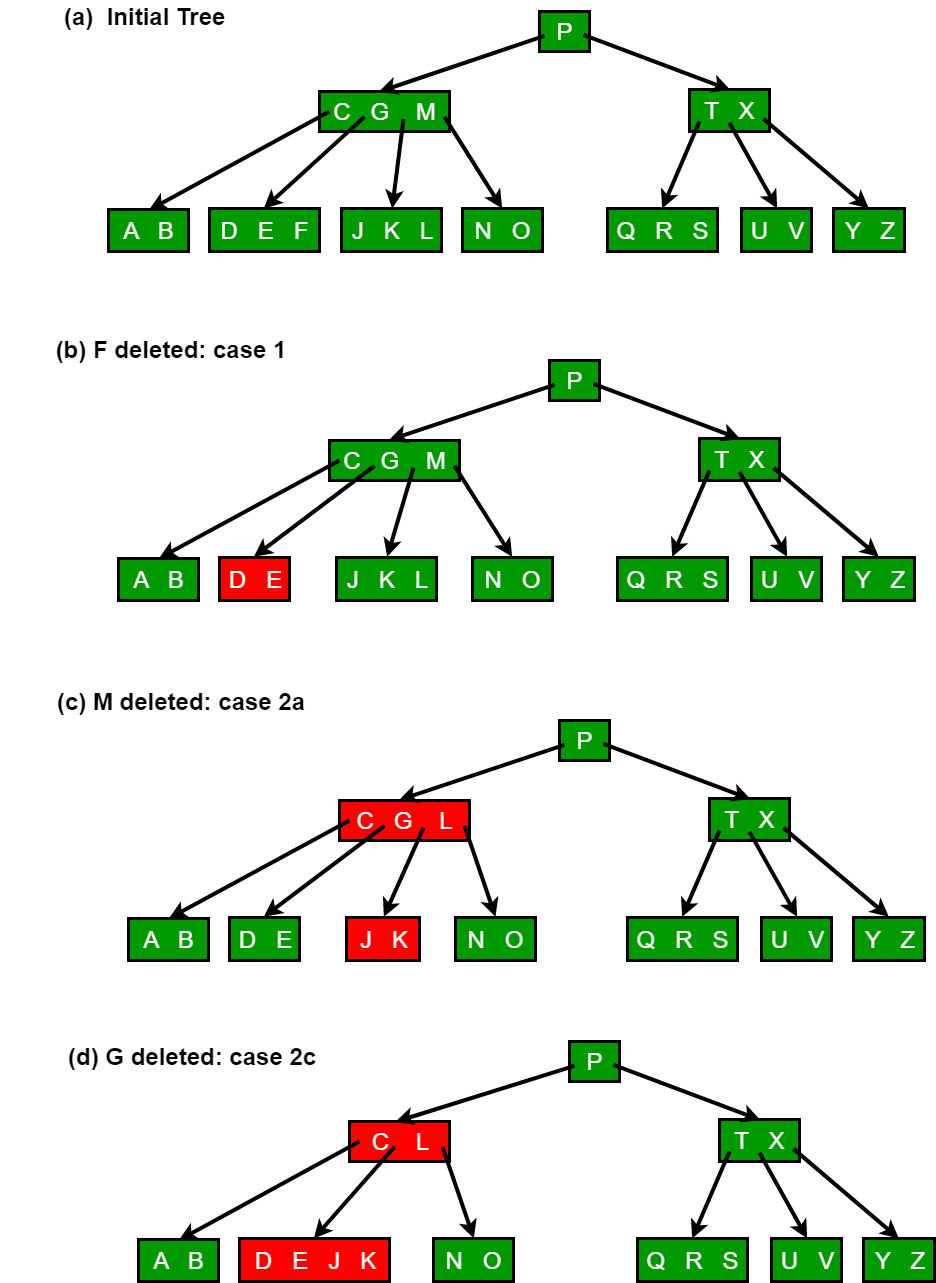
There are two special cases to consider when deleting an element:

1. The element in an internal node is a separator for its child nodes
2. Deleting an element may put its node under the minimum number of elements and children

The procedures for these cases are in order below.

Deletion from a leaf node

1. Search for the value to delete.
2. If the value is in a leaf node, simply delete it from the node.
3. If underflow happens, rebalance the tree as described in section "Rebalancing after deletion" below.

Deletion from an internal node

Each element in an internal node acts as a separation value for two subtrees, therefore we need to find a replacement for separation. Note that the largest element in the left subtree is still less than the separator. Likewise, the smallest element in the right subtree is still greater than the separator. Both of those elements are in leaf nodes, and either one can be the new separator for the two subtrees. Algorithmically described below:

1. Choose a new separator (either the largest element in the left subtree or the smallest element in the right subtree), remove it from the leaf node it is in, and replace the element to be deleted with the new separator.
2. The previous step deleted an element (the new separator) from a leaf node. If that leaf node is now deficient (has fewer than the required number of nodes), then rebalance the tree starting from the leaf node.

Rebalancing after deletion

Rebalancing starts from a leaf and proceeds toward the root until the tree is balanced. If deleting an element from a node has brought it under the minimum size, then some elements must be redistributed to bring all nodes up to the minimum. Usually, the redistribution involves moving an element from a sibling node that has more than the minimum number of nodes. That redistribution operation is called a rotation. If no sibling can spare an element, then the deficient node must be merged with a sibling. The merge causes the parent to lose a separator element, so the parent may become deficient and need rebalancing. The merging and rebalancing may continue all the way to the root. Since the minimum element count doesn't apply to the root, making the root be the only deficient node is not a problem. The algorithm to rebalance the tree is as follows:

• If the deficient node's right sibling exists and has more than the minimum number of elements, then rotate left
  1. Copy the separator from the parent to the end of the deficient node (the separator moves down; the deficient node now has the minimum number of elements)
  2. Replace the separator in the parent with the first element of the right sibling (right sibling loses one node but still has at least the minimum number of elements)
  3. The tree is now balanced
• Otherwise, if the deficient node's left sibling exists and has more than the minimum number of elements, then rotate right
  1. Copy the separator from the parent to the start of the deficient node (the separator moves down; deficient node now has the minimum number of elements)
  2. Replace the separator in the parent with the last element of the left sibling (left sibling loses one node but still has at least the minimum number of elements)
  3. The tree is now balanced
• Otherwise, if both immediate siblings have only the minimum number of elements, then merge with a sibling sandwiching their separator taken off from their parent
  1. Copy the separator to the end of the left node (the left node may be the deficient node or it may be the sibling with the minimum number of elements)
  2. Move all elements from the right node to the left node (the left node now has the maximum number of elements, and the right node – empty)
  3. Remove the separator from the parent along with its empty right child (the parent loses an element)
     • If the parent is the root and now has no elements, then free it and make the merged node the new root (tree becomes shallower)
     • Otherwise, if the parent has fewer than the required number of elements, then rebalance the parent

The following figures explain the deletion process.

Traverse

Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for remaining children and keys. In the end, recursively print the rightmost child.

Complexity

Average

Operation	Complexity
Space	O(n)
Search	O(log n)
Insertion	O(log n)
Deletion	O(log n)

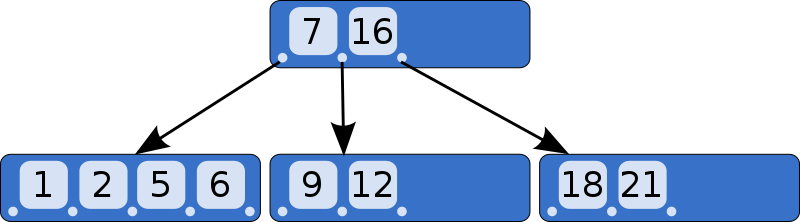
A B-tree (Bayer & McCreight 1972) of order 5 (Knuth 1998).

References

• Wikipedia
• BTech
• GeeksForGeeks
• YouTube - Fullstack Academy
• YouTube - Abdul Bari
• YouTube - saurabhschool