forked from Pozdniakov/tidy_stats
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy path360-glm.qmd
124 lines (85 loc) · 10 KB
/
360-glm.qmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
# Общая линейная модель и ее расширения {#sec-glm_general}
## Общая линейная модель {#sec-general_linear_model}
Обобщением множественной линейной регрессии можно считать **общую линейную модель (general linear model)**. Общая линейная модель может предсказывать не одну, а сразу несколько объясняемых переменных в отличие от множественной линейной регрессии.
$$Y = XB$$ где $Y$ --- матрица объясняемых переменных, $X$ --- матрица предикторов, $B$ --- матрица параметров.
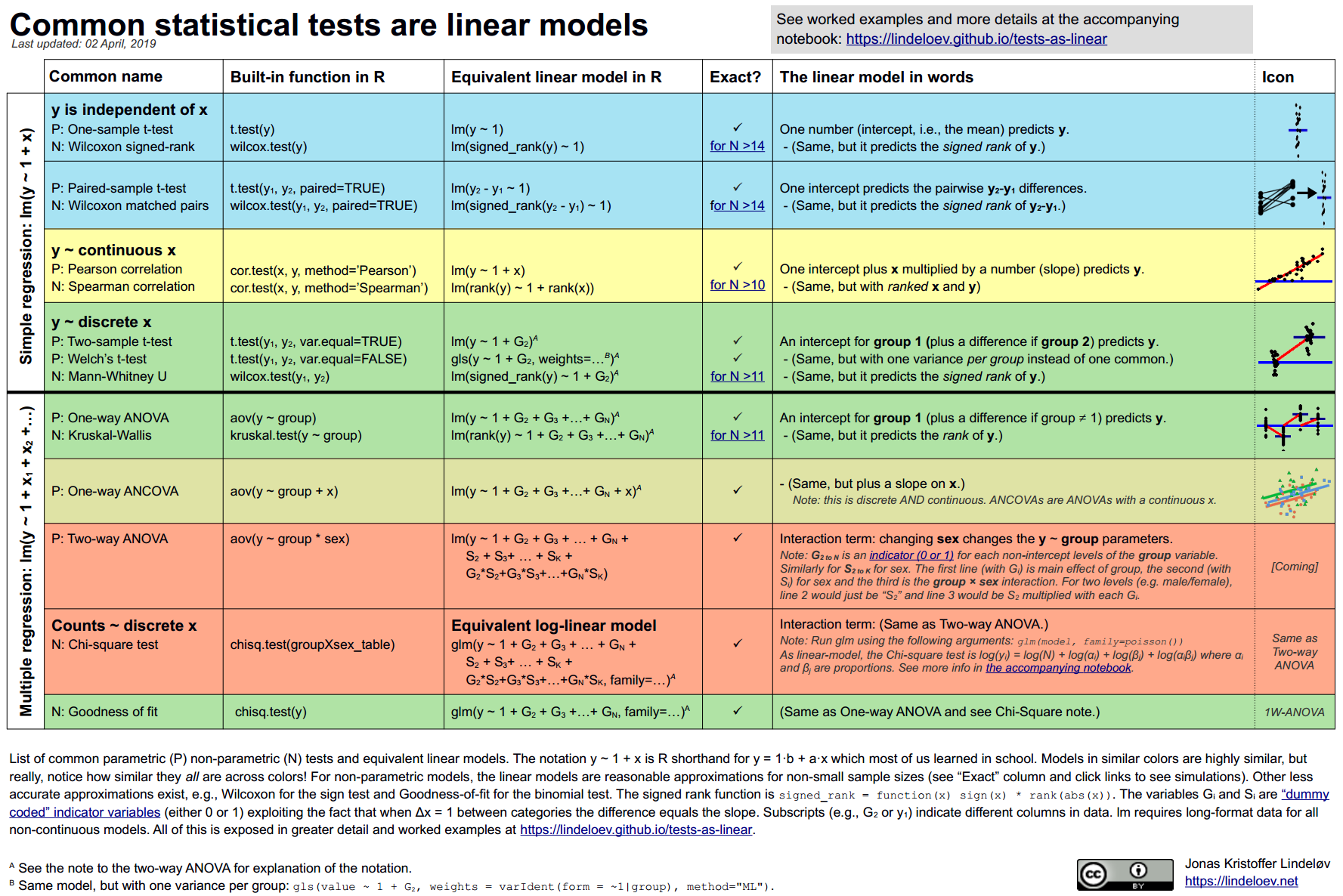
Почти все пройденные нами методы можно рассматривать как частный случай общей линейной модели: t-тесты, коэффициент корреляции Пирсона, линейная регрессия, ANOVA.
## Обобщенная линейная модель {#sec-glm_model}
**Обобщенная линейная модель (generalized linear model)** была придумана как обобщение линейной регрессии и ее сородичей: логистической регрессии и пуассоновской регрессии.
Общая линейная модель задается формулой $$Y = XB$$
Обобщенная оборачивает предиктор $XB$ **связывающей функцией (link function),** которая различается для разных типов регрессионных моделей.
Давайте попробуем построить модель, в которой объясняемой переменной будет то, является ли супергерой хорошим или плохим.
```{r}
library(tidyverse)
heroes <- read_csv("https://raw.githubusercontent.com/Pozdniakov/tidy_stats/master/data/heroes_information.csv",
na = c("-", "-99"))
heroes$good <- heroes$Alignment == "good"
```
Обычная линейная модель нам не подходит, если распределение наших ошибок далеко от нормального. А это значит, что мы не можем использовать общую линейную модель с бинарной объясняемой переменной. Эту проблему решает логистическая регрессия, которая является частным случаем обобщенной линейной модели.
Для этого нам понадобится функция `glm()`, а не `lm()` как раньше. Ее синтаксис очень похож, но нам теперь нужно задать еще один важный параметр `family =` для выбора связывающей функции (в данном случае это логит-функция, которая является связующей функцией по умолчанию для биномиального семейства функций в `glm()`).
```{r}
heroes_good_glm <- glm(good ~ Weight + Gender, heroes, family = binomial())
summary(heroes_good_glm)
```
Результат очень похож по своей структуре на `glm()`, однако вместо $R^2$ перед нами AIC. AIC расшифровывается как информационный критерий Акаике (Akaike information criterion) --- это критерий использующийся для выбора из нескольких моделей. Чем он меньше, тем лучше модель. Как и Adjusted R^2^, AIC "наказывает" за большое количество параметров в модели.
Поскольку AIC --- это относительный показатель качества модели, нам нужно сравнить его с AIC другой, более общей модели. Можно сравнить с моделью без веса супергероев.
```{r}
heroes_good_glm_noweight <- glm(good ~ Gender, heroes, family = binomial())
summary(heroes_good_glm_noweight)
```
AIC стал больше, следовательно, мы выберем модель с весом супергероев.
## Модель со смешанными эффектами {#sec-lme_model}
Модели со смешанными эффектами (mixed-effects models) --- это то же самое, что и иерархическая регрессия (hierarchical regression) или многоуровневое моделирование (multilevel modelling). Этому методу повезло иметь много названий - в зависимости от области, в которой он используется. Модели со смешанными эффектами позволяет включать в линейную регрессию не только фиксированные эффекты (fixed effects), но и случайные эффекты (random effects).
Для экспериментальных дисциплин это интересно тем, что в таких моделях можно не усреднять показатели по испытуемым или образцам, а учитывать влияние соотвествующей группирующей переменной как случайный эффект. В отличие от обычного фактора как в линейной регрессии или дисперсионном анализе (здесь он называется фиксированным), случайный эффект не интересует нас сам по себе, а его значения считаются случайной переменной.
Смешанные модели используются в самых разных областях. Они позволяют решить проблему зависимости наблюдений без усреднения значений по испытуемым или группам, что повышает статистическую мощность.
Для работы со смешанными моделями в R есть два известных пакета: `nlme` и более современный `lme4`.
```{r, eval = FALSE}
install.packages("lme4")
```
```{r}
library(lme4)
```
Для примера возьмем данные исследования влияния депривации сна на время реакции.
```{r}
data("sleepstudy")
```
Данные представлены в длинном формате: каждая строчка --- это усредненное время реакции для одного испытуемого в соответствующий день эксперимента.
```{r}
sleepstudy %>%
ggplot(aes(x = Days, y = Reaction)) +
geom_line() +
geom_point() +
scale_x_continuous(breaks = 0:9) +
facet_wrap(~Subject) +
theme_minimal()
```
Можно заметить, что, в среднем, время реакции у испытуемых повышается от первого к последнему дню. С помощью смешанных моделей мы можем проверить, различается ли скорость возрастания времени реакции от дня к дню у разных испытуемых.
Для этого мы сравниваем две модели, одна из которых является "вложенной" в другую, то есть усложненной версией более общей модели. В данном случае, более общая модель предполагает, что время реакции увеличивается у всех испытуемых одинаково, а испытуемые различаются только средним временем реакции.
```{r}
sleep_lme0 <- lmer(Reaction ~ Days + (1 | Subject), sleepstudy)
sleep_lme1 <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)
```
Визуализируем предсказания двух моделей:
```{r}
sleepstudy$predicted_by_sleep_lme0 <- predict(sleep_lme0)
sleepstudy$predicted_by_sleep_lme1 <- predict(sleep_lme1)
```
```{r}
sleepstudy %>%
rename(observed_reaction_time = Reaction) %>%
pivot_longer(cols = c(observed_reaction_time, predicted_by_sleep_lme0, predicted_by_sleep_lme1), names_to = "model", values_to = "Reaction") %>%
ggplot(aes(x = Days, y = Reaction)) +
geom_line(aes(colour = model)) +
#geom_line(aes(y = predicted_by_M1), colour = "orange") +
#geom_line(aes(y = predicted_by_M2), colour = "purple") +
geom_point(data = sleepstudy, alpha = 0.4) +
scale_x_continuous(breaks = 0:9) +
facet_wrap(~Subject) +
theme_minimal()
```
Зеленая линия (нулевая модель) имеет везде один и тот же наклон, а синяя (альтернативная модель) имеет разный наклон у всех испытуемых.
Есть несколько способов сравнивать модели, например, уже знакомый нам AIC. Кроме того, можно сравнить две модели с помощью теста хи-квадрат, восполльзовавшись функцией `anova()`.
```{r}
anova(sleep_lme0, sleep_lme1)
```
Модель со случайным наклоном прямой оказалась лучше, о чем нам говорят как более низкие AIC и BIC, так и тестирование с помощью хи-квадрат.