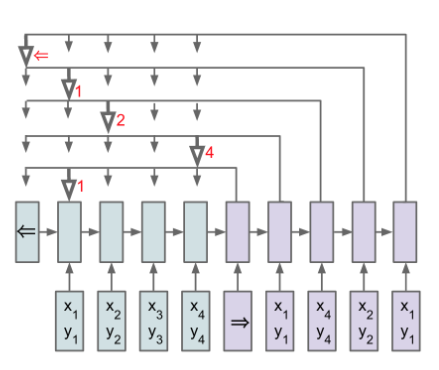
Hello and welcome to my blog! Today we are going to implement a Neural Network capable of sorting arrays of variable lengths. Note that when sorting arrays, the neural network output should refer to the input space, and therefore the output size directly depends on the input size.
After reading this short introduction a question may pop up into your mind: "What!? How can a neural network handle variable input lengths and therefore variable output sizes?". Well, we will achieve this thanks to a simple Neural Network architecture called Pointer Networks[1].
To properly understand this blog post you should be familiar with the following points (Among the points we list resources that can help you to better understand them):
- Basic PyTorch implementations - Learn more here
- Sequence2Sequence models understanding - Learn more here, here and [2].
- Attention mechanisms - Lern more here and [3]
Pointer Network (Ptr-NN) is a neural network architecture, based on sequence2sequence models, which is able to learn the conditional probability of an output sequence (Eq 1.) with elements that are discrete tokens corresponding to positions in an input sequence. Problems with this characteristics cannot be easily handled with most common architectures like simple RNN or even more complex ones as sequence-to-sequence.
Ptr-NN solves problems such as sorting arrays using neural attention mechanism. It differs from other attentions because instead of using it as a mask to weight the encoder outputs it is used as a "C pointer" to select a member of the input.
An encoding RNN converts the input sequence to a code (blue) that is fed to the decoder network (purple). At each step, the decoder network produces a vector that modulates a content-based attention mechanism over inputs. The output of the attention mechanism is a softmax distribution used to select one element of the input (Eq 2.).
The goal of our implementation is to sort arrays of variable length without applying any algorithm but forward step through out Ptr-NN.
unsorted = [5., 4., 3., 7.]
sort_array = ptr_nn(unsorted)
assert sort_array == [3., 4., 5., 7.]As we said at the 'Ptr-NN overview' the desired outputs of our function estimator are expressed using discrete tokens corresponding to the position of the input. In sorting arrays problem, our output will be the resulting tensor of applying argsort function to an unsorted array.
>>> import torch
>>> input = torch.randint(high=5, size=(5,))
>>> input
tensor([4, 2, 3, 0, 4])
>>> label = input.argsort()
>>> label
tensor([3, 1, 2, 0, 4])
>>> input[label]
tensor([0, 2, 3, 4, 4])Knowing that relation between the output and the input, we can easily create random batches of training data.
def batch(batch_size, min_len=5, max_len=10):
array_len = torch.randint(low=min_len,
high=max_len + 1,
size=(1,))
x = torch.randint(high=10, size=(batch_size, array_len))
y = x.argsort(dim=1) # Note that we are not sorting along batch axis
return x, yLet's see an small output of our data generator.
>>> batch_size = 3
>>> x, y = batch(batch_size, min_len=3, max_len=6)
>>> list(zip(x, y)) # list of tuples (tensor, tensor.argsort)
[(tensor([4, 0, 4, 0]), tensor([1, 3, 0, 2])),
(tensor([9, 7, 1, 2]), tensor([2, 3, 1, 0])),
(tensor([1, 5, 8, 7]), tensor([0, 1, 3, 2]))]The paper [1] states that no extensive hyperparameter tuning has been done. So to keep things simple we will implement an Encoder with a single LSTM layer and a Decoder with an Attention layer and a single LSTM layer too. Both Encoder and Decoder will have a hidden size of 256. The accomplish our goal we will maximize log likelihood probability with Adam optimizer with the default learning rate set by PyTorch.
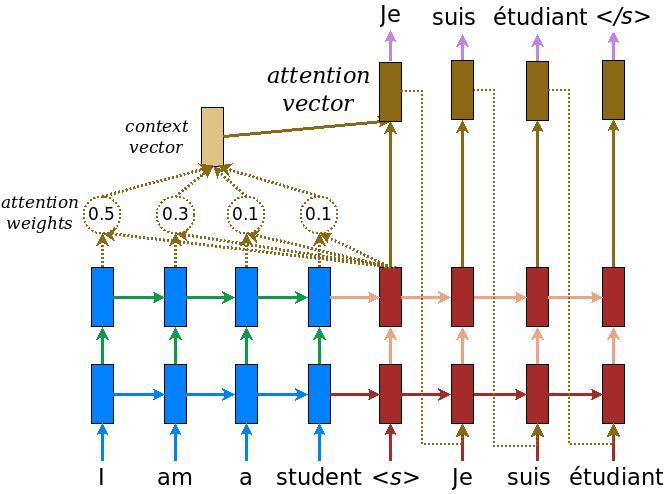 Figure 2: Seq2Seq model with attention. Similar to our Ptr-NN architecture
Figure 2: Seq2Seq model with attention. Similar to our Ptr-NN architecture
As our encoder is a single LSTM layer, we can declare it as a one-liner nn.Module.
The encoder input size is 1 because our input sequences are 1-dimensional arrays. Therefore, to make arrays 'compatible' with RNNs, we are going to feed them to our encoder reshaped to size (BATCH_LEN, ARRAY_LEN, 1).
encoder = nn.LSTM(1, hidden_size=256, batch_first=True)
# sample input
x, _ = batch(batch_size=4, min_len=3, max_len=6)
x = x.view(4, -1, 1).float()
out, (hidden, cell_state) = encoder(x)
print (f'Encoder output shape: (batch size, array len, hidden size) {out.shape}')
# Encoder output shape: (batch size, array len, hidden size) torch.Size([4, 6, 256])
print (f'Encoder Hidden state shape: (batch size, hidden size) {hidden.shape}')
# Encoder Hidden state shape: (batch size, hidden size) torch.Size([1, 4, 256])We are going to declare a new nn.Module that will implement the operations listed in the Equation 2.
The result of this implementation is an Attention layer, which their outputs are a softmax distribution over the inputs. This probability distribution is the one that the Ptr-NN will use to predict the outputs of the model.
class Attention(nn.Module):
def __init__(self, hidden_size, units):
super(Attention, self).__init__()
self.W1 = nn.Linear(hidden_size, units, bias=False)
self.W2 = nn.Linear(hidden_size, units, bias=False)
self.V = nn.Linear(units, 1, bias=False)
def forward(self,
encoder_out: torch.Tensor,
decoder_hidden: torch.Tensor):
# encoder_out: (BATCH, ARRAY_LEN, HIDDEN_SIZE)
# decoder_hidden: (BATCH, HIDDEN_SIZE)
# Add time axis to decoder hidden state
# in order to make operations compatible with encoder_out
# decoder_hidden_time: (BATCH, 1, HIDDEN_SIZE)
decoder_hidden_time = decoder_hidden.unsqueeze(1)
# uj: (BATCH, ARRAY_LEN, ATTENTION_UNITS)
# Note: we can add the both linear outputs thanks to broadcasting
uj = self.W1(encoder_out) + self.W2(decoder_hidden_time)
uj = torch.tanh(uj)
# uj: (BATCH, ARRAY_LEN, 1)
uj = self.V(uj)
# Attention mask over inputs
# aj: (BATCH, ARRAY_LEN, 1)
aj = F.softmax(uj, dim=1)
# di_prime: (BATCH, HIDDEN_SIZE)
di_prime = aj * encoder_out
di_prime = di_prime.sum(1)
return di_prime, uj.squeeze(-1)
# Forward example
att = Attention(256, 10)
di_prime, att_w = att(out, hidden[0])
print(f'Attention aware hidden states: {di_prime.shape}')
# Attention aware hidden states: torch.Size([4, 256])
print(f'Attention weights over inputs: {att_w.shape}')
# Attention weights over inputs: torch.Size([4, 6])Notice that our Attention layer is not returning the normalized (not 'softmaxed') attention weights, that is because CrossEntropyLoss will take care of first apply log_softmax and finally compute the Negative Log Likelihood Loss (NLLLoss).
The decoder implementation is straightforward as we only have to do 2 steps:
- Make the decoder input aware of the attention mask, which is computed using the previous hidden states and encoder outputs.
- Feed the attention aware input to the LSTM and retrieve only the hidden states from it.
class Decoder(nn.Module):
def __init__(self,
hidden_size: int,
attention_units: int = 10):
super(Decoder, self).__init__()
self.lstm = nn.LSTM(hidden_size + 1, hidden_size, batch_first=True)
self.attention = Attention(hidden_size, attention_units)
def forward(self,
x: torch.Tensor,
hidden: Tuple[torch.Tensor],
encoder_out: torch.Tensor):
# x: (BATCH, 1, 1)
# hidden: (1, BATCH, HIDDEN_SIZE)
# encoder_out: (BATCH, ARRAY_LEN, HIDDEN_SIZE)
# Get hidden states (not cell states)
# from the first and unique LSTM layer
ht = hidden[0][0] # ht: (BATCH, HIDDEN_SIZE)
# di: Attention aware hidden state -> (BATCH, HIDDEN_SIZE)
di, att_w = self.attention(encoder_out, ht)
# Append attention aware hidden state to our input
# x: (BATCH, 1, 1 + HIDDEN_SIZE)
x = torch.cat([di.unsqueeze(1), x], dim=2)
# Generate the hidden state for next timestep
_, hidden = self.lstm(x, hidden)
return hidden, att_w- Feed the input through the encoder, which return encoder output and hidden state.
- Feed the encoder output, the encoder's hidden state (as the first decoder's hidden state) and the first decoder's input (in our case the first token is always 0).
- The decoder returns a prediction pointing to one element in the input and their hidden states. The decoder hidden state is then passed back to into the model and the predictions are used to compute the loss. To decide the next decoder input we use teacher force only 50% of the times. Teacher forcing is the technique where the target number is passed as the next input to the decoder, even if the prediction at previous time step was wrong.
- The final step is to calculate the gradients and apply it to the optimizer and backpropagate.
To make training code more semantically understandable, we group all the forward pass in a single nn.Module called PointerNetwork.
class PointerNetwork(nn.Module):
def __init__(self,
encoder: nn.Module,
decoder: nn.Module):
super(PointerNetwork, self).__init__()
self.encoder = encoder
self.decoder = decoder
def forward(self,
x: torch.Tensor,
y: torch.Tensor,
teacher_force_ratio=.5):
# x: (BATCH_SIZE, ARRAY_LEN)
# y: (BATCH_SIZE, ARRAY_LEN)
# Array elements as features
# encoder_in: (BATCH, ARRAY_LEN, 1)
encoder_in = x.unsqueeze(-1).type(torch.float)
# out: (BATCH, ARRAY_LEN, HIDDEN_SIZE)
# hs: tuple of (NUM_LAYERS, BATCH, HIDDEN_SIZE)
out, hs = encoder(encoder_in)
# Accum loss throughout timesteps
loss = 0
# Save outputs at each timestep
# outputs: (ARRAY_LEN, BATCH)
outputs = torch.zeros(out.size(1), out.size(0), dtype=torch.long)
# First decoder input is always 0
# dec_in: (BATCH, 1, 1)
dec_in = torch.zeros(out.size(0), 1, 1, dtype=torch.float)
for t in range(out.size(1)):
hs, att_w = decoder(dec_in, hs, out)
predictions = F.softmax(att_w, dim=1).argmax(1)
# Pick next index
# If teacher force the next element will we the ground truth
# otherwise will be the predicted value at current timestep
teacher_force = random.random() < teacher_force_ratio
idx = y[:, t] if teacher_force else predictions
dec_in = torch.stack([x[b, idx[b].item()] for b in range(x.size(0))])
dec_in = dec_in.view(out.size(0), 1, 1).type(torch.float)
# Add cross entropy loss (F.log_softmax + nll_loss)
loss += F.cross_entropy(att_w, y[:, t])
outputs[t] = predictions
# Weight losses, so every element in the batch
# has the same 'importance'
batch_loss = loss / y.size(0)
return outputs, batch_lossAlso to make training steps encapsulate the forward and backward steps in a single function called train.
BATCH_SIZE = 32
STEPS_PER_EPOCH = 500
EPOCHS = 10
def train(model, optimizer, epoch):
"""Train single epoch"""
print('Epoch [{}] -- Train'.format(epoch))
for step in range(STEPS_PER_EPOCH):
optimizer.zero_grad()
x, y = batch(BATCH_SIZE)
out, loss = model(x, y)
loss.backward()
optimizer.step()
if (step + 1) % 100 == 0:
print('Epoch [{}] loss: {}'.format(epoch, loss.item()))Finally to train the model we run the following code.
ptr_net = PointerNetwork(Encoder(HIDDEN_SIZE),
Decoder(HIDDEN_SIZE))
optimizer = optim.Adam(ptr_net.parameters())
for epoch in range(EPOCHS):
train(ptr_net, optimizer, epoch + 1)
# Output
# Epoch [1] -- Train
# Epoch [1] loss: 0.2310
# Epoch [1] loss: 0.3385
# Epoch [1] loss: 0.4668
# Epoch [1] loss: 0.1158
...
# Epoch [5] -- Train
# Epoch [5] loss: 0.0836A Ptr-NN doesn't output the 'solution' directly, instead it outputs a set of indices referring to the input positions. This fact forces us to du a small post process step.
@torch.no_grad()
def evaluate(model, epoch):
x_val, y_val = batch(4)
# No use teacher force when evaluating
out, _ = model(x_val, y_val, teacher_force_ratio=0.)
out = out.permute(1, 0)
for i in range(out.size(0)):
print('{} --> {}'.format(
x_val[i],
x_val[i].gather(0, out[i]),
))
# Output: Unsorted --> Sorted by PtrNN
# tensor([5, 0, 5, 3, 5, 2, 3, 9]) -> tensor([0, 2, 3, 3, 5, 5, 5, 9])
# tensor([3, 9, 9, 7, 6, 2, 0, 9]) -> tensor([0, 2, 3, 6, 7, 9, 9, 9])
# tensor([6, 9, 4, 3, 7, 6, 4, 5]) -> tensor([3, 4, 4, 5, 6, 6, 7, 9])
# tensor([7, 3, 3, 5, 2, 4, 1, 9]) -> tensor([1, 2, 3, 3, 4, 5, 7, 9])Wow! Interesting wasn't it? In my opinion the fact that NN can solve mathematical problems is amazing. Some mathematical problems are computationally complex, but imagine that in a future we are able to train a NN to solve this complex problems and therefore simplify their computational cost.
Important takeaways
- Seq2Seq models are not only creative, they can solve mathematical problems too.
- Attention mechanism is useful for a lot of tasks, not only for NLP ones.
- Using Pointer Networks we can have a NN supporting outputs of variable sizes.
-
- Pointer Networks - Vinyals et al.
-
- Sequence to Sequence Learning with Neural Networks - Ilya Sutskever, Oriol Vinyals, Quoc V. Le
-
- Neural Machine Translation by Jointly Learning to Align and Translate - Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio